Три задания, которые не могу верно выполнить, т. к. теорию не помню. Почитала - безрезультатно. Помогите, пожалуйста.
Задание 1. Изменить порядок интегрирования

. Как мне показалось, тут 2 опечатки. 1. dy в первой части интеграла, а 2. в уравнении второй прямой. Т.к. они не образуют замкнутую область. Так?
Мое решение: После исправления возможных(?) опечаток, иначе не получилось.
 --- f(x,y) под интегралами забываете писать //AKMЗадание 2.
--- f(x,y) под интегралами забываете писать //AKMЗадание 2. Найти объем тела, ограниченного поверхностями:

,
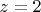
,

,

.
Мое решение: Получился параболоид, симметричный относительно

, ограниченный сверху плоскостью
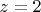
и пересеченный плоскостями

.
Пределы интегрирования:

.

.
Нашла ошибку в вычислениях. Ответ конечный не пишу.
Задание 3. Вычислить интеграл по замкнутому контуру:

. Контур С:

. Непосредственно и по формуле Грина.
Мое решение: Получилась парабола, ограниченная сверху прямой

. Т. к.

, значит имеем полный дифференциал функции 2 переменных и выбираем путь интегрирования произвольно. Берем правую часть параболы. Кривая:

. Интеграл равен -12. Но т. к.

, интеграл по левой части параболы равен 12. И конечный интеграл равен

. По формуле Грина
 -- Ср апр 10, 2013 06:07:07 --
-- Ср апр 10, 2013 06:07:07 --Во 2 задании получила




