Не очень хорошо разбираюсь в этой теме, но хочу помочь, поэтому выскажу свои соображения.
Согласно лемме о накачке, приведенной в википедии, для регулярного языка существует константа

такая что для любого слова языка

не короче

имеется представление

причем

Ну попробуем доказать от противного, поскольку имеются слова сколь большой длины в языке,
то какое бы

мы не подобрали, всегда придется допускать, что слово

непусто, иначе просто берем слово длиннее и оно не представимо в виде

Таким образом, в языке

должны иметься слова вида

для всех натуральных
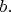
Но это невозможно, так как найдется такое

что

ни для каких

Это попробуйте доказать самостоятельно.
-- 09.04.2013, 13:34 --Я заметил небольшую неувязку в своем доказательстве, но возможно вы немного ошиблись с условием, потому что приведенный вами язык очевидно регулярный. Так как при

в него войдут все слова любой длины больше двух, а регулярность такого языка вполне очевидна. Другое дело, если

тогда приведенное мной доказательство сработает.



