Рассмотрим следующую задачу





Второе неравенство показывает, что движение происходит в области

т.е в задаче присутствует стенка

.
Первое неравенство означает, что помимо

на частицу действуют еще какие-то силы направленные от стенки

.
Наконец произведение равное 0 означает, что эта дополнительная сила возникает только на стенке.
Иными словами при взаимодействии с частицей стенка способна создавать силы направленные в область

.
Поскольку вторых производных у решения вообще говоря нет, данные соотношения надо понимать в смысле распределений. Но мы сейчас на этом не будем особо останавливаться, поскольку наша цель -- построение примеров неединственности. А для этого достаточно и нестрогих формулировок.
В такой формулировке решений может быть великое множество. Ну действительно, все эти неравенства никак не регулируют величину реакции стенки. Так что при ударе частица может остановиться или отразиться с
какой угодно скоростью. Поэтому необходимо как-то ограничить этот произвол. На мой взгляд вопрос этот довольно сложный. Но один случай выглядит сравнительно простым. Потребуем, чтобы удар был абсолютно упругим. В этом случае скорость после удара должна быть равна скорости до удара с противоположным знаком. Или, другими словами, квадрат скорости - непрерывен. Нетрудно сообразить, что такое требование приводит к интегральному тождеству

Добавим это тождество к предыдущим соотношениям и зададимся вопросом существования и единственности решения поставленной задачи.
Уже доказательство существования решения не слишком тривиальная задача. Метод штрафа дает оценку на

. Оценок на

не ожидается (первая производная терпит разрывы). Но в вариационном неравенстве фигурирует

, поэтому слабой сходимости недостаточно. Кроме того, надо еще и разбираться с законом сохранения энергии. Однако все это преодолимо и в конце концов можно доказать существование такого решения.
Займемся единственностью решения. Простые примеры вполне обнадеживают - решение единственно. Попробуем это доказать. Стандартный подход выглядит так. Пусть у нас имеются два решения

. Рассмотрим их разность

. Тогда эта разность удовлетворяет соотношениям



И все, тупик. После интегрирования слева не возникает положительно определенная форма. И ничего доказать не удается.
И вот тут выясняется замечательный факт. Пусть какая-нибудь такая функция
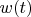
существует. Тогда существуют примеры неединственности. А именно, задача




имеет два решения. Одно из этих решений

, а другое

.
Да, в правой части стоят срезки. Поэтому данные в правой части вообще говоря негладкие. Может быть все дело в гладкости? Нет, гладкость здесь не поможет.
Отметим, что конкретно для данного уравнения (оператор двойного дифференцирования) можно предъявить и более простой пример : функции

, а другое

являются решениями задачи




Позже мы увидим, что
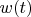
- бесконечно осциллирует возле 0. На вид она похожа на функцию типа

. Этот пример выглядит совсем симпатично. В начальный момент частица покоится на стенке. Затем на частицу начинает действовать некая специально подобранная
прижимающая сила. Одно из решений очевидно - частица так и покоится. Но есть и другое решение - частица по этакой раскачивающейся "синусоиде" отходит от стенки и вновь возвращается. В этом решении происходит бесконечное количество ударов об стенку. При этом энергия сохраняется и скорость падения равна скорости отражения.
Но вернемся к первому примеру. Он носит более общий характер и позволит нам построить решения без ударов. Предположим, что нам удалось найти такую
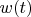
, что

и

- гладкие функции. Тогда гладкие функции

являлись бы решниями задачи




В результате мы получим два гладких решения задачи с гладкой правой частью. Это и означает, что ударов об стенку нет. Данный подход годится и для негладких

, но тогда получаются решения "с ударами" (в правой части некие

- функции).
Увы. Такую функцию
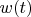
вряд ли удастся найти. Но идея именно такая. Позже мы вернемся к этому вопросу.
Итак, все дело свелось к построению функции
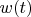
со свойством

. Простейший пример -
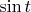
. Но увы. Надо еще и обнуление производной в 0. Но идея уже понятна. Рисуем этакую синусоиду с бесконечным колебанием стягивающуюся к 0. При этом там где функция положительна - график вогнутый, а там где отрицательна -выпуклый. Если не заботиться о гладкости то и вообще можно взять пилу с кусочно линейным графиком.
Поправим это дело. Загладим эту пилу там, где она ломается. Данная функция
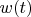
нужное количество раз дифференцируема и линейна в некоторой окрестности каждого своего нуля (там где обращается в 0).
И вот теперь, если взять функцию

как результат заглаживания

в тех самых окрестностях, то получим, что

и

являются решениями задачи




Дальше уже как и выше получаем два гладких решения и для задачи с ограничением

. Да, там надо еще повозиться, получить оценки, но это уже дело техники.
Данный подоход позволяет строить примеры неединственности и для более общих операторов. Например для интегральных операторов типа дробного дифференцирования порядка больше 1.



