Ну так вот, случай плоского пространства-времени соответствует случаю
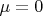
, что попадает под случай

, а Вы меня обругали.
Каким образом "попадает", объясните пожалуйста? Таким, что вы не смогли решить правильно тривиальное неравенство

?
Впрочем, обругал я вас не за то, что вы решать неравенства не умеете - а за то, что никакого физического смысла решениям придать не можете. Попробую последний раз достучаться до вашего спящего разума... Подумайте, пожалуйста, что изменится, если вы совершите преобразование координат

. Как изменится интеграл для уравнения геодезической, как изменится ваше неравенство, как изменятся ваши "выводы"?
Я не знаю, что там у Someone за метрика и насколько она обща, но мне, неспециалисту, кажется...
Я могу вам только посоветовать делать в случае "кажется" - то, что делают все безграмотные люди, креститься.
что должен появиться какой-то размерный эффект.
Предъявите соответствующий масштабный фактор, пожалуйста.
Если взять нить большой, но конечной длины

, то в задаче появится еще несколько длин. На больших расстояниях от нити

(это второе характерное расстояние) она будет "видеться", как точечная масса М, для которой можно составить гравитационный радиус

(это третье характерное расстояние). Для малых абсолютных величин массы гравитационный радиус будет, конечно, меньше

и чернодырного решения не будет - решение будет слабосильным и "в присутствии вещества" и сшивается по другому. Но для больших величин

гравитационный радиус может с лихвой перекрыть

и тогда может появиться некое чернодырное решение с "исчезнувшим" в дыре веществом.
Все, на этом месте физика кончилась - далее пошли сопли...
Вариации

для данной длины

в значительной степени моделируются вариациями

бесконечной нити на данном расстоянии

.
ротор поля наподобие дивергенции градуирует себя вдоль спина и там, внутре, обращает материю вопроса в спиритуальные электрические вихри, из коих и возникает синекдоха отвечания...
Поэтому я думаю, что возможно образование горизонта при конечном

даже для бесконечной нити.
Не думаю, что сильно ошибусь - если скажу что ваши "думания" уже не интересны не только мне, но и всем остальным присутствующим. Т.к. облечь их в связные физические рассуждения, предъявить выкладки вы не пытаетесь.
Для такой нити "правый конец" и "левый конец" создают взаимно компенсирующие поля, эффективно сводя бесконечную нить с бесконечной полной массой к конечному отрезку

конечной массы

.
Вам, извините, как барану - несколько раз уже указали на то, что "двумерная" гравитация - существенно отличается от трехмерной. Вторая космическая скорость - равна бесконечности, асимптотика потенциала - совсем другая. Но этот упертый, извините, баран - продолжает "эффективно сводить" несводимые вещи к очередному бреду...



