Да, этой подсказки действительно недостаточно. В том решении, которое я знаю, ещё используется теорема Бэра. Впрочем, можно и без неё, "на пальцах".
1. Докажите первое утверждение 1, сформулированное выше. Это несложно. (Там h будет зависеть от t и от

,

).
2. Теперь нам бы хотелось видоизменить утверждение 1 следующим образом: надо как-то заменить отрезок
![$[t,t+h]$ $[t,t+h]$](https://dxdy-02.korotkov.co.uk/f/9/1/6/916d4cc91589793cd5549fd026fe5e6382.png)
на интервал, содержащий точку

. Если бы мы могли предъявить хотя бы одну точку
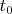
такую, что для любого
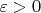
существует окрестность

точки
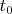
, такая что
из

вне

следует

,
то мы бы сразу выписали последовательность функций

, сходящихся к нулю по метрике, но не поточечно.
Предположив, что мы уже нашли точку
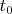
, проделайте это (предъявите искомую последовательность

).
3. Дело за малым - найти
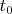
. Назовём точку

"хорошей для

", если для фиксированного

она обладает свойством: функции

, обращающиеся в ноль вне некоторой окрестности точки

, имеют метрику

.
Точку, которая является "хорошей" для бесконечно малой последовательности эпсилонов, назовём "совсем хорошей". Искомая точка
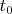
- как раз и есть "совсем хорошая".
Обозначим множество точек, "хороших для

", через

.
Пользуясь уже доказанным пунктом 1 из этого сообщения, для любого фиксированного

предъявите множество

. Докажите, что это будет почти весь отрезок.
4. Последний шаг: рассмотрите пересечение

. Докажите, что оно не пусто. Точка, лежащая в этом пересечении, и будет нужной нам "совсем хорошей".