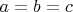Лажа в использовании неравенства Коши, в доказательстве которого предполагается, что a и b мы выбираем произвольно. Но тогда они не будут удовлетворять условиям (то, что мы к целевой функции прибавили правую часть ограничения и отняли левую - не значит, что оно стало выполняться).
Нестрогое решение сходу:
Условие и целевая функция не меняются при перестановке a, b, c. Очевидно, решение достигается при
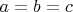
, то есть

(тут, конечно, может быть ситуация, что экстремум достигается на границе - но граница недостижима, вот если бы в условии было "неотрицательных", то минимальное значение 0)
Далее очевидно, что ЦФ=63.
Решение через Лагранжа:

при условии


Ищем производные и приравниваем к нулю.




И опять выходим на