Двое бросают монету

[qx87]

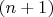
Первый бросает $n$ раз, второй — $(n + 1)$ раз. Какова вероятность, что у второго выпадет больше орлов?

Ответ: ${1 \over 2}$.

Интуитивное объяснение: в среднем случае у второго есть лишь один дополнительный бросок, чтобы реализовать преимущество, и вероятность выпадения орла в этом броске: ${1 \over 2}$. Конечно, оно совсем не строгое.

Ещё одно объяснение: положим $n = 0$, тогда вероятность равна ${1 \over 2}$. Но здесь ещё нужно доказать, что вероятность не зависит от $n$.

Правильно математическое решение пытался вывести и по индукции, и через представление результатов бросков цепочками битовых строк, и через определение вероятности. Чуть осязаемого результата добился только третьим способом — получил зубодробильное выражение ${1 \over 2^{2n + 1}} \cdot \sum\limits_{k = 1}^{n + 1}\left({C_{n + 1}^k \cdot \sum\limits_{i = 0}^{k - 1}C_n^i}\right)$, которое тождественно равно ${1 \over 2}$, но доказать это тоже не получается, даже по индукции.

[Shadow]

Так как второй бросает "еще один раз", то у него или орлов будет больше, или решек (но никак и те и другие). Какова вероятность, что болше будет именно орлов?

[mihailm]

Shadow в сообщении #686418 писал(а):

Так как второй бросает "еще один раз", то у него или орлов будет больше, или решек (но никак и те и другие).

Далее соображения симметрии - каждому случаю когда орлов больше поставим в соответствие...

[qx87]

Блин, такое элементарное решение!
Спасибо большое.