Простите за сумбур, начну сначала.
Постановка задачи:пусть

независимы.

одинаково распределены с общей симметричной абсолютно непрерывной функцией распределения

.

целочисленная неотрицательная с.в.

при

.

. Пусть существуют числа

такие, что

. Показать, что
![$\lim_{n\to\infty}P\{X_{[N/2]}^{(N)}<a_nx\}=E\Phi{(x \sqrt{\xi})$ $\lim_{n\to\infty}P\{X_{[N/2]}^{(N)}<a_nx\}=E\Phi{(x \sqrt{\xi})$](https://dxdy-04.korotkov.co.uk/f/f/d/f/fdfe930ed0d897ecd65668ed06a7a96f82.png)
.
![$X_{[N/2]}^{(N)}$ $X_{[N/2]}^{(N)}$](https://dxdy-04.korotkov.co.uk/f/3/d/1/3d105953b910d50a60593ab1e4e1db7e82.png)
порядковая статистика ранга
![$[N/2]$ $[N/2]$](https://dxdy-02.korotkov.co.uk/f/d/0/0/d006a5c12069ad51438deee25ede2bfa82.png)
построенная по выборке случайного объема

.
Указание. Использовать соотношение

.

имеет биномиальное распределение

. Далее применить т. Муавра-Лапласа.
Методом статистического моделирования построить гистограмму величины
![$T_n=X_{[N/2]}^{(N)}/a_n$ $T_n=X_{[N/2]}^{(N)}/a_n$](https://dxdy-04.korotkov.co.uk/f/7/d/f/7df9d6f958120e76d2ed114259b2c76f82.png)
и сравнить ее с плотностью предельного распределения.
В задании 2 варианта:
1.

,

,
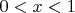
.
2.

имеет отрицательное биномиальное распределение

,

равномерное распределение на отрезке (-1,1).



