Я собираюсь порешать задачки по графам далее из домашних заданий.
Задача 4.1. В графе с

вершинами степени вершин равные

. При том

. Докажите, что в графе есть гамильтонов цикл.
Доказательство.Воспользуемся теоремой Поше.
Пусть 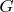 имеет
имеет  вершин. Если для всякого
вершин. Если для всякого  , число вершин со степенями, не превосходящими n, меньше чем n, и для нечетного
, число вершин со степенями, не превосходящими n, меньше чем n, и для нечетного  число вершин степени
число вершин степени  не превосходит
не превосходит  , то
, то  — гамильтонов граф.
— гамильтонов граф.Подробнее тут:
http://rain.ifmo.ru/cat/view.php/theory ... onian-2005Попробуем опровергнуть условие задачи. Пусть есть граф

для которого выполнено неравенство для степеней вершин. Сделаем граф максимально негамильтоновым (добавление любого ребра сделает его гамильтоновым). Если мы докажем, что граф будет иметь гамильтоновый цикл даже в том случае, когда мы сказали что он "максимально насыщенный", то получиться, что мы докажем противоречие. Тогда если мы добавляли какое-то ребро, предполагая что после этого граф стал насыщенный, но еще не гамильтоновый, то мы не могли добавлять ни одного ребра, а он уже был насыщенный. И опятьже, если он был изначально насыщенный, а мы доказали что он имеет г.цикл, то так и получим противотечение.
(Оффтоп)
При том, если изначально был граф, в котором выполнялось условие задачи, а потом добавилось новое ребро, то все равно условие задачи будет выполняться: если где-то неравенство нарушилось, то мы можем всегда отсортировать последовательность, а сумма от этого не уменьшиться (мы ведь только увеличиваем степени), т.к. до добавления ребра последовательность тоже была отсортирована.
Теперь пусть

- насыщенный. Еще раз, добавление любого ребра приведет к появлению г.цикла. Это гарантирует наличие г.пути между любыми двумя вершинами (иначе противоречие). Тогда если первая вершина не соединена с вершиной

(нумеруем в порядке возрастания степени), то автоматически получится г.цикл (был г.путь между всеми парами вершин), здесь пользуюсь критерием Дирака.
Но

, значит первая вершина соединена и с вершиной

.
Теперь, если посмотреть на любую вершину из первой половины последовательности, то видно, что


и т.д.
Поэтому получаем аналогичными рассуждениями для всех вершин, что

для всех

Теперь в точности выполняется критерий Поше. Значит, противоречие.
Вот теперь мне не понятно почему здесь написано именно

P.S. может я пишу много, да еще и неправильно или неточно. Мне такие доказательства немного непривычны.



