Добрый день.
Захотелось разобраться в следующей задаче: как будет вести себя показатель адиабаты при изохорическом нагреве постоянной массы двухатомного газа от температуры

до

, где I - энергия диссоциации. Ниже изложены мои соображения по этому поводу, нет ли там грубых ошибок?
Считаем газ идеальным. Пусть

- начальное химическое количество газа, и при температуре

диссоциировала доля частиц

. Тогда имеем

двухатомных молекул и

одноатомных молекул. Внутренняя энергия равна

Полная теплоёмкость

Примем для простоты

Тогда производная

и окончательно

Введём для краткости записи обозначение

. Тогда из определения показателя адиабаты имеем:

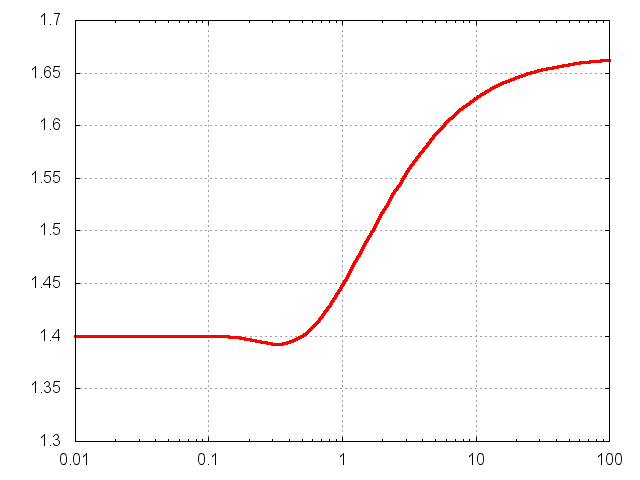
График полученного выражения выглядит так (по оси

отложена температура в единицах

):
Как и ожидалось, при

выполняется

, а при

асимптотика

. Несколько неожиданным было немонотонное поведение показателя адиабаты, но оно вполне объяснимо. Кстати, если считать

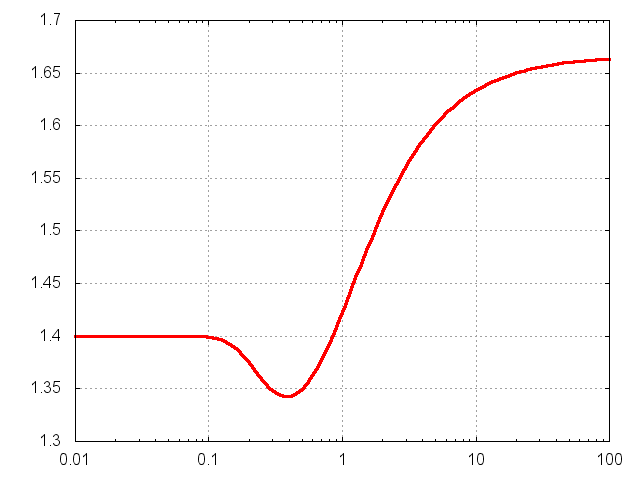
по формуле

(она верна для идеального газа с фиксированным числом степеней свободы), то получается другое выражение:


Асимптотики у него тоже правильные, но переход между ними иной (хотя тоже немонотонный):