есть цепь
http://s2.ipicture.ru/uploads/20121209/3jP4EvjU.jpgсловами:
цепь подключена к источнику
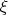
. В цепи есть две параллельные ветви. В каждой ветве два последовательных конденсатора(в первой

, во второй

,

:

и

.
Чему равна разность потенциалов

между точками А и B? точка А находится между

и

, B - между С

и

.
я знаю, как выразить напряжения конденсаторов через напряжение на источнике и через емкости конденсаторов.
не понятно другое: почему

?
будем считать положительным направлением обхода контура движение слева направо.
из закона Ома для участка цепи:

или

(в первом слагаемом знак минус, потому что мы обходим контур против положительного направления).
не могу понять, где я ошибся.
моя формула:

формула из решебника:

я свою формулу могу обосновать, если расставить потенциалы:





подставив разности потенциалов под соответствующие напряжения, получим верное равенство.
в чем проблема? и еще я не могу понять, почему стоят модули в формуле из решебника.



