Здравствуйте. Вот такая задача попалась на производстве.
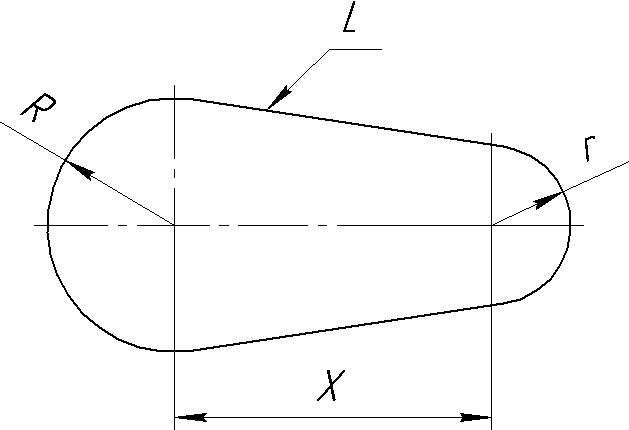
Это два грубо говоря колеса с известными радиусами. Также известна длина "ремня", опоясывающего оба колеса.

мм. Требуется найти

(то есть межцентровое расстояние)
Как решали мы с другом:
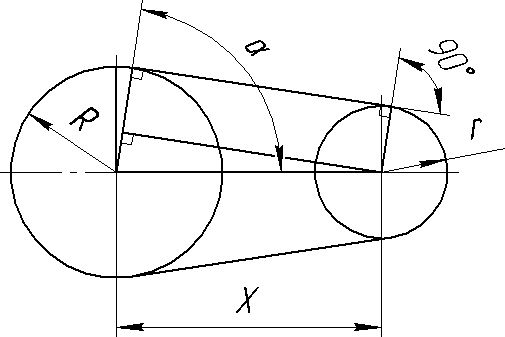
Ввели угол альфа и пишем систему уравнений
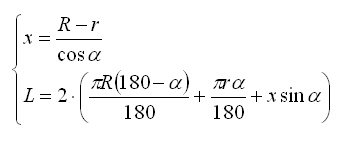
Первое выражение – понятно.
Во втором первые два слагаемые – вывод длин дуг через угол альфа, третье слагаемое – длина касательного к двум окружностям отрезка.
При решении этой системы после упрощений и подстановок вылезло уравнение типа

. Как его решать я ума не приложу.
Либо может подскажете более лёгкий способ вывода

?



