Можно через представление пифагоровых троек попробовать.
представимо в виде суммы двух квадратов натуральных чисел (это следует из теоремы Ферма-Эйлера). То есть
.
). Докажем тождество
А доказательство самой теоремы могу в оффтоп кинуть. В иностранных источниках Zagier's "one-sentence proof", почему-то именно это док-во мне нравится больше всего. Хотя есть более короткое, через детерминанты, но не вникал.
Рассмотрим преобразование, которое тройке натуральных чисел

сопоставляет три числа

по следующему правилу:

если


если


в остальных случаях.

Обозначим это преобразование буквой

:

Очень легко проверить,что преобразование

сохраняет форму

Для случая

имеем:

Для случая

имеем:

Для случая

имеем:

Значит, если для какого-то числа

имелось равенство

, то оно сохранится и после преобразования

.
Проверим, что преобразование

, дважды примененное, возвращает нас назад.
Проделаем это для случая

.
Пусть

, тогда

, откуда

и, значит,

надо вычислять по правилу

:



И в остальных случаях все аналогично.
А теперь предположим, что

– простое число вида

. Тогда, во-первых, уравнение

разрешимо, по крайней мере, двумя способами:

или

. И, во-вторых, это уравнение имеет конечное число решений. Если предположить, что среди его решений нет таких, при которых

(ведь если таковы имеются, то и доказывать нечего:

), мы получим, что преобразование

разбивает все решения на пары:

, если только

. Посмотрим, существуют такие пары или имеются ли у преобразования

неподвижные точки.
Очень легко понять, посмотрев на формулы

, что неподвижные точки у

– те, для которых

. Но при

решений у уравнения

нет (ибо

не кратно

). Значит, есть только одна неподвижная точка

. Из всего сказанного вытекает, что число решений уравнения

нечетно: неподвижная точка

, а остальные решения разбиваются на пары.
Однако есть еще одно преобразование, обозначим его

, которое

и

меняет местами:

. Посмотрим, какие тройки (из наших решений уравнения

) оно оставляет на месте, то есть каковы те

, что

.
Мы условились ранее, что

. Но тогда и неподвижных точек нет! Значит, все решения разбиваются на пары. То есть число решений четно! Но только что мы утверждали, что число решений нечетно. Получилось противоречие. Значит, обязано существовать решение уравнения

, где

, то есть

– сумма двух квадратов. Мы доказали, что простое число
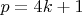
представимо в виде суммы двух квадратов натуральных чисел.
, кстати, Вы думали о той задаче (произведение чисел в строках и столбцах таблицы)?



