Большой модуль очень
Но он получается рассмотрением отдельно по модулю 5 и 8. Так же, как объяснил
Cash. И он мог сказать "по модулю 24..." (тоже большой). А ваше решение какое?
Вот моё:
а) Если
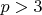
, то почти так же, как сказал Cash :
Смотрим по модулю 8. Если

, то правая часть делится на 8. Тогда

и

должны быть чётными. Но тогда по модулю 3 не получается.
б) Если

и

, смотрим по модулю 10. Тогда х чётно, но тогда не прокатывает по модулю 8. Единственное решение (0, 1, 1).
в) Если

- сводится к уравнениям

и

Первое не прокатывает по модулю 27 (единчтвенное решение (0 1 1))
Второе не прокатывает по модулям 10 и 3.
Простите, что написала неразьорчиво, торопилась. Если что-то непонятно, спрашивайте.
До вторника времени ещё туча.



