Приятного Вам отдыха

Спасибо!
Давайте для удобства изменим обозначения и будем говорить о такой задаче:
найти положительный минимум для  , где
, где  ,
,  --- произвольные натуральные числа.
--- произвольные натуральные числа. Пусть

--- явное решение уравнения

в области

(
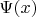
можно найти, например, по формуле Кардано, но это неважно). Легко понять, что искомый минимум находится среди значений вида
![$f(k,[\Psi(k)]+1)$ $f(k,[\Psi(k)]+1)$](https://dxdy-01.korotkov.co.uk/f/c/5/e/c5ef15a3804bf18c2f941a9df79242e582.png)
, где

пробегает весь ряд натуральных чисел. Главная трудность состоит в том, что зависимость
![$[\Psi(k)]$ $[\Psi(k)]$](https://dxdy-03.korotkov.co.uk/f/2/1/1/21125eb9ded5f80f80031991891fd38e82.png)
от

, хоть и близка к линейной, не является линейной, при этом отклонения от линейности довольно трудно учесть. Вы это пытались делать, вводя дополнительный параметр

, а основным параметром у Вас было

--- отношение коэффициентов при

в формулах для

и

. Число

довольно близко к правильному коэффициенту линейной зависимости, равному

(это точное значение тангенса угла наклона асимптоты к графику функции

), поэтому до некоторого момента у Вас всё складывалось благополучно, а дальше случилось то, что случилось. Конечно, можно заменить

другим конкретным
рациональным числом, более близким к
иррациональному числу

, но это не поможет по аналогичным причинам. Вот если бы асимптота к кривой

имела рациональный тангенс угла наклона, Ваша идея вполне бы сработала (попробуйте таким способом аккуратно найти положительный минимум для, например,

--- здесь успех обеспечен). Более того, если этот тангенс иррационален, но всего лишь
квадратично, то также можно выкрутиться (например, мы можем элементарно и сравнительно просто найти положительный минимум для

), однако соответствующий метод непригоден для
кубических иррациональностей, каковой является

. Это, конечно, даёт некоторую призрачную надежду, но не более.
И ещё одно замечание. Сведение решения исходного уравнения к задаче о положительном минимуме представляется довольно дорогим удовольствием. Если изначально нужно было доказать неразрешимость всего лишь одного уравнения, то теперь фактически придётся доказывать неразрешимость всех уравнений вида

, где

(т.е. вместо одной редьки получаем без малого две сотни таких же, как бы это помягче выразиться, ...

).