1. Найти последние три цифры числа

.
2. Доказать, что число

не является разностью кубов двух натуральных чисел.
3. Пусть

есть высота прямоугольного треугольника, опущенная на его гипотенузу, а

- радиус вписанной в этот треугольник окружности. Найти первую цифру после запятой в десятичной записи отношения

.
4. На горизонтальной плоскости лежат четыре шара радиуса

, а их центры образуют квадрат со стороной

. Сверху в лунку, образованную этими шарами, положили пятый шар такого же радиуса. Найти расстояние от его высшей точки до плоскости.
5. Решить в положительных числах систему
 -- 08.11.2012, 20:21 --
-- 08.11.2012, 20:21 --Сегодня был на этой олимпиаде. Я вот понять не могу... Либо я глупый и ничего не соображаю в математике, либо из-за того, что мои усилия в постижении сией науки приходятся на ночную часть дня, я жестоко тормозил. Почему мне так не даются утренние олимпиады?!
В первой задаче разложил факториал,
сократил со знаменателем,
представил в каноническом виде (в виде произведения степеней простых чисел),
проследил на что заканчиваются степени множителей канонического представления (исключил пятерку),
перемножил последние цифры,
полученное произведение опять представил в каноническом виде,
помножив на пять, последовательно получил последние цифры

.
И самое главное, потом я, переписывая на чистовик, зачем то написал вместо нулей везде пятерки. Нормально? То есть описав два листа решения везде пишу типа: "так как четное число, оканчивающиеся на

умножается на пять, то его последняя цифра

"! Какого.... интеграла:evil: (попытался пошутить)
Во второй тоже сглупил, как можно было забыть (или точнее забыть проверить, я не знаю, что это было), что

?? Задача элементарнейшая

Третью не смотрел, всего два часа было выделено, сейчас буду думать.
Четвертую лень всю описывать. Рассмотрел вид сверху, потом вид сбоку, где виден желобок (лунка). Ответ получился

. Скорее всего не правильно, делалось все на скорую руку, много времени ушло на первую задачу, где я написал пятерки (первый раз такое чувство испытываю).
Пятое. нашел такие решения

и

, где

. Ну а если ни одно из чисел не равняется единице, тогда логарифмируем, подставляем, получаем

, потом в исходном домножаем и имеем
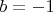
и по-цепочке все остальные, которые не удовлетворяют условию.



