Поставлена задача приблизить стандартное нормальное распределение

распределением Коши в смысле минимизации максимального отношения

. Нужно найти оптимальные параметры Коши

и

.
Получается

Достаточно очевидно (в силу симметрии и того, что пики распределений будут совпадать), что
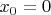
(и более того, это должно быть правильным ответом). Если принять это предположение, то задача достаточно легко решается поиском производных по

, потом по

.
Вот только обосновать слова "в силу симметрии" пока не получается. Неплохо было бы, например, поменять местами max и min, но функция не удовлетворяет теореме о минимаксе.
Что еще можно попробовать сделать?



