Комбинаторика. Млита. Булевы функции.

[ogcjm]

Всем привет. Требуется проверить верно ли решение и ответить на 1 маленький вопрос в конце текста.

Условие задачи: найти число булевых функций от n переменных таких, что в их сднф любая элементарная конъюнкция содержит хотя бы 2 отрицания.

Рассуждаю так:

Каждой элементарной конъюнкции в сднф соответствует набор на котором функция принимает значение 1. В конъюнкциях в сднф будет хотя бы 2 отрицания, если каждая из этих конъюнкций строится не на наборах:
1. Единичный набор, т.к. ему соотв. конъюнкция без отрицаний.
2.Набор с одним нулём, т.к. такому набору соотв. конъюнкция с 1 отрицанием. Количество таких наборов равно $n$.

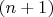
Следовательно, на $(n + 1)$ наборе, функция заведомо равна нулю. Таким образом осталось
$(2^{n} - 1 - n)$ "свободных наборов".

Отсюда получаем, что количество функция удовлетворяющих условию задачи равно:

$2^{2^{n} - 1 - n}$. (1)

Но, если функция равна нулю, то для неё не существует сднф, и следовательно от (1) надо отнять ещё единицу. Верно ли это?

[cyb12]

Да, все верно.
Однако, если функция равна 0, то тут некоторые люди говорят, что сднф для нее имеет вид $x_1\bar x_1,$ но она, впрочем, тоже не подходит и единицу все равно следует вычесть.