В этом году придумал задачу, которую сам до конца не решил:
Условие: четырёхугольник

. Вокруг треугольников

и

описаны окружности, пересекающие

и

в точках

и

соответственно (соотвественно окр.1 и окр.2); окр.2 пересекает диагональ четырёхугольника

в точке

;
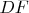
пересекает

в точке

; окр.1 пересекает диагональ

в точке

;

пересекает

в точке

.
Доказать или опровергнуть: треугольники

и

гомологичны.

и

как вписанные. Следовательно,

. Следовательно, прямые

и

параллельны. (теорема о вписанном угле, признак параллельности прямых). Т.к.

параллелен

,

как накрест лежащие,и

как вписанные=> D, H, G и С лежат на одной окружности. Углы DGH и HCD равны как вписанные так же, как и углы ECD и EBD (окр.2). Тогда

(J-пересечение прямой

и окр.2). Но

,

,

,

лежат на окр.1, поэтому

,

,

лежат на одной прямой.

. Следовательно, отрезок

параллелен

.
Поначалу это и требовалось доказать. Затем возникла гипотеза.
 -- 07.10.2012, 11:13 --
-- 07.10.2012, 11:13 --
В общем, треугольники не гомологичны, вопрос только, всегда или не всегда.
Вопрос открытый: всегда ли данные треугольники не гомологичны?



