Пусть

. Докажите, что:

(примечание)
Равенство здесь достигается не только когда
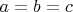




Будем искать минимум функции методом Лагранжа


Возьмем частные производные в такой комбинации:


На первый множитель можно сократить

В этом выражении три раза повторяется дробь. Обозначим её функцией



Функция f - вогнутая, поэтому две из трех переменных должны быть равны друг другу.

Вернемся к исходному неравенству. Пусть y=z.

Это решается совсем просто возведением в квадрат

У функции четыре минимума: (1,1,1), (9/5,3/5,3/5), (3/5,9/5,3/5), (3/5,3/5,9/5)
В каждом минимуме функция равна 24.



