Исправление
------------------
Относительная дифферента идеала

называется относительной дифферентой поля поля

исправляется на:
Относительная дифферента идеала

называется относительной дифферентой поля

Исправление
------------------
Пусть

- дробный идеал поля

.
Дуальным к

называется множество

всех таких чисел

поля

, что относительный след произведения

является целым алгебраическим числом, для любого числа

, принадлежащего дробному идеалу

.
То есть,

.
исправляется на:
Пусть

- дробный идеал поля

.
Дуальным к

называется множество

всех таких чисел

поля

, что относительный след произведения

является целым алгебраическим числом, для любого числа

, принадлежащего дробному идеалу

.
То есть,

.
Исправление
------------------
Чтобы доказать, что некоторое множество

чисел поля

является дробным идеалом, нужно доказать, во-первых, что

является

-модулем, и, во-вторых, что существует такое целое алгебраическое число

, что

.
исправляется на:
Чтобы доказать, что некоторое множество

чисел поля

является дробным идеалом, нужно доказать, во-первых, что

является

-модулем, и, во-вторых, что существует такое ненулевое целое алгебраическое число

, что

.
Исправление
------------------
Но, в некоторых случаях, доказать, что

-модуль

является конечно-генерируемым может быть труднее, чем найти такое целое алгебраическое число

, что

.
В этих случаях, находят такое

, и, таким образом, устанавливают, что

- дробный идеал.
исправляется на:
Но, в некоторых случаях, доказать, что

-модуль

является конечно-генерируемым может быть труднее, чем найти такое ненулевое целое алгебраическое число

, что

.
В этих случаях, находят такое

, и, таким образом, устанавливают, что

- дробный идеал.
-------------------------------------------------------------------------------------------------------------
Пусть

- конечное расширение числовых полей,
![$[K:F]=n$ $[K:F]=n$](https://dxdy-04.korotkov.co.uk/f/b/9/9/b995efc6642a3030cf96b0f7bc0c974682.png)
.
Пусть

, где

- целое алгебраическое число.
Пусть

- кольцо всех целых алгебраических чисел поля

.
Пусть

- кольцо всех целых алгебраических чисел поля

.
Пусть

- мономорфизмы из поля

в поле

комплексных чисел, оставляющие поле

неподвижным.
Пусть

, ...,

- какой-либо

-базис поля

.
Пусть матрица

Относительным дискриминантом

-базиса

, ...,

называется число:

,
то есть квадрат детерминанта матрицы

.
Это определение относительного дискриминанта

-базиса аналогично определению абсолютного детерминанта

-базиса.
Относительный дискриминант любого

-базиса поля

принадлежит полю

и не равен нулю.
Это доказывается точно так же, как в случае абсолютного дискриминанта

-базиса.
Сначала рассматривается относительный

-базис состоящий из чисел:

,

,

, ...,

(где целое алгебраическое число

генерирует поле

:

).
Относительный дискриминант этого базиса является квадратом детерминанта Вандермонда, который принадлежит полю

и не равен нулю в силу сапарабельности расширения полей

.
Матрица перехода от одного

-базиса поля

к другому является обратимой и её детерминант не равен нулю.
Из этого следует, что относительный дискриминант любого

-базиса поля

принадлежит полю

и не равен нулю.
Если

-базис

, ...,

состоит из целых алгебраических чисел (принадлежащих кольцу

), то относительный дискриминант этого

-базиса является целым алгебраическим числом, принадлежащим кольцу

.
Лемма
----------
Пусть

, ...,

-

-базис поля

.
Тогда

.
Доказательство
-------------------
Пусть

- мономорфизмы из поля

в поле

комплексных чисел, оставляющие поле

неподвижным.
Пусть матрица

.
Тогда

.
Следовательно,

,
что и требовалось.
Лемма
---------
Пусть

- какой-либо дробный идеал поля

.
Тогда в

cуществует

-базис поля

, состоящий из целых алгебраических чисел.
То есть существуют такие числа

, ...,
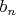
, принадлежащие дробному идеалу

и одновременно кольцу

, что

, ...,
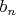
-

-базис поля

.
Доказательство
--------------------
Пусть

- какой-либо ненулевой элемент дробного идеала

, являющийся целым алгебраическим числом (то есть одновременно элементом кольца

).
Тогда относительная норма

принадлежит дробному идеалу

.
Доказывается это точно таким же способом, как и в случает абсолютной нормы.
Пусть

- относительный характеристический полином числа

.
Поскольку

, то коэффициенты этого полинома являются целыми алгебраическими числами (принадлежащими кольцу

), поэтому свободный член

принадлежит дробному идеалу

, значит и относительная норма

принадлежит дробному идеалу

.
Пусть теперь

, ...,

- какой-либо

-базис поля

, состоящий из целых алгебраических чисел (принадлежащих кольцу

).
Тогда числа

, ...,

образуют требуемый

-базис поля

.
Лемма
----------
Пусть

- какой-либо дробный идеал поля

.
Пусть

- дуальное множество:

.
Тогда существует такое ненулевое целое алгебраическое число

, что

.
Доказательство
---------------------
Пусть

, ...,
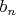
- какой-либо

-базис поля

, принадлежащий дробному идеалу

и одновременно кольцу

(такой

-базис поля

существует согласно предыдущей лемме).
Пусть

- какое либо число, принадлежащее дуальному множеству

, где числа
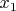
, ...,
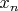
принадлежат полю

.
Тогда
(1)

, ...,

.
Запишем условия (1) в виде равенств:
(2)

,
...

,
где

, ...,

- некоторые числа, принадлежащие

.
Числа
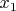
, ...,
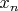
можно найти из равенств (2) по правилу Крамера.
Поскольку детерминант

равен дискриминанту базиса

, то этот детерминант принадлежит кольцу

и не равен нулю.
Каждое из чисел
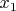
, ...,
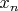
равно отношению детерминантов двух матриц, элементами которых являются целые алгебраические числа, принадлежащие

.
Пусть

.
Тогда

, ...,

и

.
Следовательно

(поскольку

).
Поскольку

- произвольный элемент дуального множества

, то

, что и требовалось.
Лемма
----------
Пусть

- какой-либо дробный идеал поля

.
Пусть

- дуальное множество:

.
Тогда

является дробным идеалом.
Доказательство
--------------------
В силу предыдущей леммы осталось доказать, что

является

-модулем.
Если

и

, то

и

, для любого числа

, следовательно

.
Значит

, для любого числа

, следовательно

.
Значит

- абелева группа по сложению.
Если

и

- произвольное число кольца

, то

, следовательно

.
Значит

, следовательно

.
Значит

-

-модуль, что и требовалось.