RIP писал(а):
Capella писал(а):
Ответ:

При

в общем случае ответ неверен.
Не знаю, пока остаюсь при своём мнении. Там всё зависит от пересечений, вероятно надо посмотреть более подробно на числах (причём при достаточно большом

относительно

). Например для

и
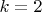
ответ верен, например одно из правильных решений:

и формула работает -

Интересно проверить для

и

 Добавлено спустя 18 минут 32 секунды:
Добавлено спустя 18 минут 32 секунды:
Мне кажется мы ещё как то по разному понимаем условие.

У меня складывается впечатление, что Вы делаете вот такой вариант:
1 группа: {12}, {123}
2 группа: {13}, {123}
3 группа: {23}, {123}
Отсюда делается вывод, что подмножеств 4: {12},{23},{13},{123}
Но ведь тогда не выполнятеся условие, что у
любых двух подмножеств количество одинаковых элементов k. Ключевое слово здесь "любые", оно должно быть отнесено
ко всем 4 подмножествам.



