1.
В задаче склейки внутреннего решения с внешним вакуумным решением Рейсснера-Нордстрема в работе (ЖЭТФ 128, 2, 2005, с.300) ошибок нет.
(чтобы не перемещаться по топику, некоторые формулы, уже приведенные в теме, здесь дублируются)
Доказательство.
а) Краткое.
В данной теме выше было показано, что из решения уравнений Эйнштейна-Максвелла для внешнего вакуумного гравитационного поля сферически симметричного массивного заряженного тела массы покоя

с зарядом

следует, что это поле в системе отсчета, в которой оно покоится, описывается в общем случае статической метрикой (теорема Биркгофа), определенной с точностью до произвольной функции

:
(1)

,
где

,

- гравитационный радиус источника,

- т.н. критический радиус,

- постоянная Эйнштейна,

- полная гравитационная энергия заряда,

.
Её определитель равен

,
и он обращается в нуль, помимо точек
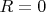
(сингулярной точки пространства),

(особых точек сферической системы координат, в которых она «вырождается», т.к. в них неопределена циклическая координата

), ещё и в точках, где

,

, где данная система координат также вырождается, но уже по другой причине : вблизи этих точек обращаются в нуль ковариантные компоненты вектора перемещения вдоль радиальной координаты :

.
Тем не менее, все геометрические характеристики – кривизны поверхностей в этих точках - определены однозначно. В частности,
2-гауссова кривизна сфер, ортогональных координатам

:

;
4-кривизна этих же сфер :
(2)

;
Её производная по радиальной координате :
(3)

;
4-кривизна 2-поверхностей, ортогональных координатам

:

.
Здесь

- классический радиус.
Метрика (1) может быть подвергнута произвольным взаимно однозначным гладким преобразованиям, оставляющим инвариантной геометрию :

,

,-
с не равными нулю якобианами прямого и обратного преобразований.
В рамках статических метрик (1) производную

, не равную нулю тождественно, можно выбрать произвольно. В частности, при :
1)

получаем метрику Рейсснера-Нордстрема (теорема Биркгофа для массы с зарядом) :
(4)

;
2) В работе (ЖЭТФ 128, 2, 2005, с.300) выбрана система координат для вакуумной метрики, в которой производная

обращается в нуль при

, т.е. в месте будущей склейки внутреннего мира электрического заряда, имеющего горловину при

, с этим вакуумным его продолжением.
В частности, в качестве примера рассмотрена функция :

,

,
равная

на горловине.
Такая система координат, как обосновано выше, допустима, хоть и вырождается на горловине из-за обращения в нуль на ней определителя метрики. При этом, как уже было отмечено, все геометрические величины на горловине остаются однозначно определёнными и конечными.
Единственное замечание, которое надо сделать : при приведении метрики (1) к метрике (4) Рейсснера-Нордстрема, т.е. при преобразованиях данных координат с

(назовём их координатами Толмана) к координатам кривизн (Шварцшильда) c

,

, якобиан преобразования

нулится на месте склейки, т.е. на горловине. Но т.к. это происходит в одной точке на границе области, то, как было замечено в ходе дискуссии
Someone’м, это не нарушает изометричности. Смысл этой особенности состоит в том, что в координатах кривизн из-за условия

(в качестве радиальной координаты выбирается 2-скаляр – радиус гауссовой кривизны поверхностей радиальных сфер) экстремум кривизны, которому соответствует условие

, ими не описывается.