Добрый вечер!
В теме, посвящённой периметрам целочисленных треугольников, была высказана следующая лемма:
Если у различных целочисленных треугольников равного периметра одна одинаковая сторона, у них не может быть равных углов.
Эта лемма может быть не верна. Доказанные случаи не объемлют всего множество случаев. В самом деле, остался незамеченным случай, когда равны углы, из которых один прилежит к неподвижной стороне, а один не прилежит.
Для этого случая удалось только вывести формулу: пусть у треугольников

и
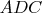
общая сторона

,

,

,

,

a,


В итоге получилось только для отдельных случаев.
C уважением, Николай



