Для целого положительного n и натурального m, обозначим через

количество всех решений уравнения

в целых числах

(решения

и

считаются одинаковыми, только при равенстве кортежей, т.е.

. Найдите сумму
![$\sum_{i=-[\sqrt{n}]}^{[\sqrt{n}]} (n-(m+1)i^2)S_m(n-i^2)$ $\sum_{i=-[\sqrt{n}]}^{[\sqrt{n}]} (n-(m+1)i^2)S_m(n-i^2)$](https://dxdy-04.korotkov.co.uk/f/f/4/4/f44799971952e83e7691cbe0db700d8e82.png)
Задача взята из отборочного этапа 15 всеукраинского турнира юных математиков (школьников) имени Ядренко.
Собственно вопрос: как определить функцию S? Под знаком суммы, естественно, ничего не упрощается (разве что можно заменить диапозон индекса удвоением результата). При
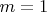
S определенна естественным образом. При

следует из известных формул. Для

или

вопрос открыт. Для

можно применить решение

, опираясь на теорему Лагранжа о сумме четырех квадратов, где C принимает все значения, удовлетворяющие неравенству:

, где

принадлежит множеству целых чисел.
Какие идеи будут по нахождению общего вида функции S?



