Как доказать, что для любой положительной последовательности, которая стремится к нулю, мы можем построить ограничивающую ее сверху выпуклую последовательность, которая тоже стремится к нулю?
Подходящей мажорирующей последовательностью

была бы, например, "кусочно-линейная" последовательность, которая на каждом следующем куске линейного убывания имела бы меньший наклон, чем на предыдущем. Ну подобного рода последовательность организуется довольно очевидным образом.
Например, так. Определим

и

, где

-- это максимум вообще всех иксов. Потом положим

таким, чтобы все

при всех

были бы меньше, чем

, и определим

. Потом определим
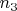
из двух соображений: при всех

должно быть

и при этом

, а

положим равным

. И вообще: каждый следующий

определим так, чтобы выполнялось

и, кроме того,

при всех

, а

положим равным

.
Так вот: теперь если доопределить

линейно зависящими от номера на каждом промежутке между соседними

, то ровно нужная мажоранта и получится.
(если я в записи индексов/степеней не сбился; но если даже и сбился, то это легко поправить)



