Министерство образования и науки Украины
Институт инновационных технологий и содержания образования
XLVII Всеукраинская олимпиада юных математиков
Первый день
8 класс
8.1. Решите систему уравнений:

8.2. На шахматной доске

в левом нижнем углу стоит ладья. Двое игроков ходят по очереди. Первый за один ход передвигает ладью на любое количество клеток по вертикали вверх или вниз, а второй - по горизонтали вправо или влево. Если во время игры ладья пересекла клетку (останавливалась на ней или проходила через нее), то еще раз пересекать такую клетку запрещается. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает в этой игре?
8.3. В равнобедренном треугольнике

(
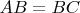
)

. На сторонах

и

выбраны точки

и

соответственно. Оказалось, что отрезок

перпендикулярен стороне

и равен половине стороны

. Докажите, что

.
8.4. Обозначим через

количество натуральных делителей числа

. Найдите все пары натуральных чисел

, которые удовлетворяют уравнению:
 9 класс
9 класс
9.1. При каких действительных значениях параметра

неравенство

выполнено при всех действительных значениях

?
9.2. На прямоугольной клетчатой доске в левом нижнем углу стоит ладья. Двое игроков ходят по очереди. Первый за один ход передвигает ладью на любое количество клеток по вертикали вверх или вниз, а второй - по горизонтали вправо или влево. Если во время игры ладья пересекла клетку (останавливалась на ней или проходила через нее), то еще раз пересекать такую клетку запрещается. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает в этой игре, если доска имеет размеры
а)

;
б)

(2006 клеток по вертикали)?
9.3. Найдите все пары натуральных чисел

, удовлетворяющие уравнению:

9.4. Внутри треугольника

с углами

и

имеется такая точка

, что

,

,

. Найдите длину отрезка

.
10 класс
10.1. Смотри задачу 9.1.
10.2. В остроугольном треугольнике

проведены высоты

и

. На лучах

и

за точками

и

выбраны точки

и

соответственно так, что

. Радиусы окружностей, вписанных в треугольники

и

, равны. Обязательно ли треугольник

равнобедренный?
10.3. На клетчатой доске размером

двое игроков по очереди рисуют многоугольники (не обязательно выпуклые) единичной площади с вершинами в узлах сетки. Запрещается рисовать многоугольник, имеющий общие точки с уже нарисованными. Проигрывает тот, кто не может нарисовать очередной многоугольник. Кто выигрывает в этой игре?
10.4. Найдите все функции

, удовлетворяющие для всех чисел

уравнению:

если множество

является множеством:
а) всех целых чисел;
б) всех рациональных чисел.
11 класс
11.1. Фигура на координатной плоскости задана уравнением:

Доказать, что эта фигура имеет центр симметрии, и найти его координаты.
11.2. Смотри задачу 10.2.
11.3. Пусть

- такой многочлен, что

для всех натуральных

. Найдите

.
11.4. Найти все функции

, удовлетворяющие условиям:
1) для всех действительных значений

,

выполнено равенство:

;
2) уравнение

имеет единственное решение.
ЗАДАЧИ ПРЕДЛОЖИЛИ: Гоголев Андрей (8.1, 8.3), Рублев Богдан (8.2, 9.2, 10.3), Петровский Дмитрий (8.4), Лишунов Виталий (9.1, 10.1), Торба Сергей (9.3), Чубенко Алексей (9.4), Клурман Алексей (10.2, 11.2, 11.4), Туркевич Эдвард (10.4), Малицкий Юрий (11.1), Рыбак Александр (11.3).
Министерство образования и науки Украины
Институт инновационных технологий и содержания образования
XLVII Всеукраинская олимпиада юных математиков
Второй день
8 класс
8.5. Найти все пары целых чисел

, удовлетворяющие уравнению:

8.6. Могут ли при некотором действительном значении

одновременно быть рациональными числа

и

?
8.7. Упорядоченную пару чисел

разрешается заменить на одну из следующих четырех пар:

при

,

при

.
а) Получите с помощью этих операций из пары

пару

.
б) Докажите, что при любом способе получения из пары

пары

в некоторый момент была получена пара с одной нулевой компонентой.
8.8. На каждой стороне треугольника

во внешнюю сторону построены равносторонние треугольники:

,

и

. Через середины отрезков

,

и

провели прямые, перпендикулярные сторонам

,

и

соответственно. Докажите, что проведенные прямые пересекаются в одной точке.
9 класс
9.5. В выпуклом семиугольнике

параллельными являются отрезки:

и

,

и

,

и

,
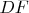
и

,

и

и

и

. Докажите, что отрезки

и

также параллельны.
9.6. Смотри задачу 8.7.
9.7. В выпуклом 2007-угольнике все стороны и диагонали покрашены в один из

цветов. Произвольные три вершины многоугольника задают такой треугольник, что по крайней мере две его стороны имеют одинаковый цвет. Найдите все значения

, при которых такое раскрашивание возможно.
9.8. Решите систему уравнений:

если параметр

удовлетворяет условию:
1)

;
2)

.
10 класс
10.5. Решите неравенство:

10.6. В стране Карнавалии 669 городов, некоторые из которых соединены дорогами с односторонним движением. Каждый день в произвольных двух городах проводят карнавал, на время которого все дороги, входящие и выходящие из этих городов, перекрываются. Но схема дорог в Карнавалии устроена так, что жители других 667 городов могут проехать из любого одного города в любой другой, воспользовавшись одной или несколькими дорогами, не нарушая правил движения. Какое наименьшее количество дорог может быть в Карнавалии?
10.7. В остроугольном треугольнике

угол

равен

. Точка

принадлежит стороне

. Докажите неравенство:

10.8. Докажите, что для произвольных разных простых чисел

и

уравнение

а) имеет ровно два решения в натуральных числах

;
б) в обоих решениях значения

одинаковы.
11 класс
11.5. Доказать, что существует бесконечное количество таких натуральных чисел

, что каждый из промежутков

не содержит ни одного числа вида

,

,

, где

- натуральное число.
11.6. Смотри задачу 10.6.
11.7. Пусть

,

- набор разных чисел из промежутка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Обозначим через

среднее арифметическое всех возможных произведений разных

элементов набора. Докажите, что последовательность

невозрастающая.
11.8. В остроугольном треугольнике

проведена биссектриса

, точка

- ее середина. На отрезке
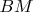
существует такая точка

, что угол

равен

, на отрезке

существует такая точка

, что

. Докажите, что точки

,

,

,

принадлежат одной окружности.
ЗАДАЧИ ПРЕДЛОЖИЛИ: Лишунов Виталий (8.5, 10.5), Торба Сергей (8.6), Аникушин Андрей (8.7, 9.6), Чубенко Алексей (8.8, 10.7), Туркевич Эдвард (9.5, 10.8, 11.7), Клурман Алексей (9.7, 11.8), Рыбак Александр (10.6, 11.6), Петровский Дмитрий (9.8, 11.5)
Решения (на украинском языке):
http://infostore.org/file/3010543/2513646/Ukr2007.djvu 1,238,882
Решения и список победителей (на украинском языке):
http://www.forux.ho.com.ua/vseykr_2007.rar (.DOC) 252,139



