Обозначим

. Докажем, что эта функция - искомая.
1)

- равномерно непрерывна на

.
Действительно, выберем любое

. Так как K равностепено непрерывно, то существует

.
Возьмем любые

. Пусть для определенности

. Так как

, то существует

. Очевидно также, что

.
Тогда

.
2)

.
Выберем любое

. Так как K равностепено непрерывно и

- равномерно непрерывна, то существует

.
Выберем множество точек

. Для

.
Построим функцию

. Возьмем произвольное
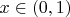
, а через

обозначим ближайшее к
![$x$ [math]$x_i$ $x$ [math]$x_i$](https://dxdy-01.korotkov.co.uk/f/4/d/1/4d196eebac78ae28a3bf1dc589c8303282.png)
. Тогда

и, следовательно:

.
Таким образом получаем, что в любой окрестности f(x) имеется функция из K, следовательно f(x) принадлежит замыканию K, а так как K замкнуто, то

, чтд.



