1) При диагностике заболевания пациента врач с вероятностью 0,95 диагностирует заболевание F и с вероятностью 0,05 заболевание G. Для уточнения диагноза он отправляет больного на дополнитнльный анализ, который с вероятностью 0,45 дает положительную реакцию в случае заболевания F и с вероятностью 0,17 в случае заболевания G. Результаты анализа оказались положительными. Какова вероятность, что жто было заболевание G?
2) Из колоды с 36 картами одну за другой вынимают 2 карты. Случайное событие А="Первая вынутая карта валет пик", случайное событие В="Обе вынутые карты красной масти" Напишите определение несовместных случайных событий и ответьте на вопрос, какими булут случайные события А и В: совместными или совместными? Напишите определение независимых случайных событий и ответьте на вопрос: зависимы ли случайные события А и В. Все ответы должны быть обоснованы
======================================
1) Я так думаю, что эта задача на формулу Байеса.

- пациент болен
Можно ли построить гипотезы так?

- врач диагностирует первично на заболевание F

- врач диагностирует первично на заболевание G

- доп анализ на заболевание F
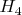
- доп анализ на заболевание G
Тогда необходимо найти

?
Верно ли, что

?
2)События

и

-- несовместны, так как их пересечение представляет пустое множество.


То есть

=> события

и

- зависимые.
Верно?



