Интересно узнать мнения опытных математиков о составлении олимпиадных задач. Какой наиболее оптимальный набор задач для 10-11 классов. Я имею ввиду очные туры олимпиад по математике (уровня Всеукраинских). И речь идет именно об украинских олимпиадах, потому как в России, я заметил, несколько другие задачи.
Как пример выкладываю задачи с очного тура одной из олимпиад в Украине.(уровень 10 класса)
1. Решить уравнение
![$$\sqrt[3]{\sqrt[5]{x}-1}+\sqrt[3]{\Big( \sqrt[5]{x}-1 \Big)^3 - \sqrt[5]{x} + 2}=\sqrt[15]{x}+\sqrt[3]{\Big( \sqrt[5]{x}-1 \Big)^3 - \sqrt[5]{x} + 1}.$$ $$\sqrt[3]{\sqrt[5]{x}-1}+\sqrt[3]{\Big( \sqrt[5]{x}-1 \Big)^3 - \sqrt[5]{x} + 2}=\sqrt[15]{x}+\sqrt[3]{\Big( \sqrt[5]{x}-1 \Big)^3 - \sqrt[5]{x} + 1}.$$](https://dxdy-04.korotkov.co.uk/f/3/0/3/3037cadc35b01c5779e1c1c7fbd3590682.png)
2. Дан острый угол

и точки

и

во внутренней области угла. Найти на стороне
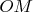
точку

так, чтобы треугольник

, где точки

- точки пересечения прямых

и

с

был равнобедренным.
3. Дано шесть цифр:

. Найти сумму всех четырехзначных четных чисел, которые можно записать с помощью этих цифр. В этих числах цифры могут повторяться.
4. Пусть

,

,

. Доказать, что существует такое число

, что для любого натурального


5. Доказать, что для любых разных целых чисел

существует бесконечно много таких натуральных

что числа

являются попарно взаимно простыми.



