Пусть

- числовое поле, где

- целое алгебраическое число.
Пусть
![$[F:\mathbb{Q}]=n$ $[F:\mathbb{Q}]=n$](https://dxdy-02.korotkov.co.uk/f/5/0/0/50059ceab7893c0195fced4269defce082.png)
.
Пусть

- кольцо всех целых алгебраических чисел поля

.
Пусть

- какое-либо непустое множество идеалов кольца

.
Идеал

называется максимальным в

, если он не содержится ни в каком другом идеале из

.
Если

- множество всех собственных идеалов кольца

, то максимальный идеал в

является максимальным идеалом кольца

.
Лемма
-----------
Пусть

- какое-либо непустое множество идеалов кольца

.
Тогда существует максимальный идеал (возможно не один) в

.
Доказательство
------------------------
Предположим обратное.
Тогда существует бесконечная цепочка
(1)

идеалов из

, в которой никакие два соседних идеала не равны.
Пусть

- объединение всех идеалов этой цепочки.
Множество

является идеалом кольца

, следовательно конечно-генерируемой абелевой группой по сложению.
Пусть

, ...,

- генераторы этой абелевой группы идеала

.
Все идеалы цепочки (1), начиная с некоторого, содержат все элементы

, ...,

, следовательно содержат идеал

.
Поскольку эти идеалы также содержатся в

, то они равны

, в противоречии с тем, что соседние идеалы цепочки (1) не равны.
Пусть

и

- два множества чисел из поля

.
Произведением множеств

и

называется множество чисел поля

, представимых конечной суммой произведений вида

, где

,

(среди слагаемых могут быть одинаковые).
Это произведение множеств коммутативно и ассоциативно.
Чтобы доказать ассоциативность заметим, что

и

являются множеством чисел поля

, представимых конечной суммой произведений вида

, где

,

,

.
Лемма
-------------
Пусть
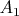
, ...,

- множества целых алгебраических чисел из кольца

.
Пусть

- простой идеал кольца

.
Если произведение множеств

содержится в

, то хотя бы одно из этих множеств содержится в

.
Доказательство
-------------------------
Сначала докажем лемму для

.
Предположим обратное:

,

,

.
Тогда существуют два числа

и

, ни одно из которых не принадлежит идеалу

.
Произведение

принадлежит

, следовательно принадлежит

, в противоречии с тем, что

- простой идеал.
Пусть теперь

.
Предположим обратное, и пусть

- наименьшее целое число большее

-ух, для которого утверждение леммы неверно.
Тогда

, значит

.
В силу минимальности

, одно из множеств
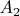
, ...,

содержится в

в противоречии с предположением.
Лемма
-----------
Если

и

- группы по сложению, то их произведение

является группой по сложению.
Доказательство
------------------------
Разность двух конечных сумм произведений вида

, где

,

является конечной суммой произведений этого вида, поскольку

и

.
Значит разность двух чисел из

принадлежит

, следовательно

является группой по сложению.
Лемма
----------
Если

и

- идеалы, то их произведение

является идеалом.
Доказательство
------------------------
Множество

содержит только целые алгебраические числа.
В силу предыдущей леммы,

является группой по сложению.
Пусть

- какое-либо целое алгебраическое число, а

- какое-либо число из

.
Покажем, что

.
Число

является конечной суммой произведений вида

, где

,

.
Поскольку

и

, то

, что и требовалось.
Суммой идеалов

и

называется множество чисел вида

, где

и

.
Сумма идеалов

и

является идеалом.
Лемма
----------
Пусть

,

,

- идеалы.
Тогда

.
Доказательство
----------------------------
Конечная сумма произведений вида

, где

,

,

равна сумме двух конечных сумм: конечной суммы произведений вида

, где

,

, и конечной суммы произведений вида

, где

,

.
Поэтому

.
Поскольку

и

, где

,

, то

.
Поскольку

и

, где

,

, то

.
Следовательно,

.
Значит

.
Пусть

, ...,

- какой-либо набор элементов кольца

.
Пусть

- множество элементов вида

, где

, ...,

- произвольные элементы кольца

.
Множество

является идеалом, содержащим элементы

, ...,

.
Этот идеал назвается генерируемым элементами

, ...,

и обозначается

.
Главными идеалами называются идеалы , генерируемые одним элементом.
Главные идеалы обозначаются

или

, где

- генератор идеала.
Лемма
-----------
Любой идеал

содержит произведение конечного числа простых идеалов (которое может состоять и из одного сомножителя).
Доказательство
------------------------
Предположим обратное.
Пусть

- множество всех идеалов, которые не содержат произведение конечного числа простых идеалов.
Пусть

- максимальный идеал в множестве

(которое непусто по предположению).
Идеал

не является простым по предположению, следовательно существуют такие целые алгебраические числа

и

, не принадлежащие идеалу

, что

.
В силу максимальности

в

, идеалы

и

не принадлежат

, т.е. содержат произведения конечного числа простых идеалов.
Следовательно идеал

содержит произведение конечного числа простых идеалов.
Но

, что противоречит принадлежности идеала

множеству

.
Лемма
------------
Пусть

- какой-либо собственный идеал кольца

.
Тогда существует такое алгебраическое число

, не являющееся целым, что

.
Доказательство
-----------------------
Пусть

- какой-либо ненулевой элемент идеала

.
Имеем:
(2)

,
где

, ...,

- простые идеалы, существующие в силу того, что идеал

содержит произведение простых идеалов, а

- простой идеал, существующий в силу того, что среди собственных идеалов кольца

, содержащих

, есть максимальный.
Пусть

- наименьшее колличество простых идеалов, произведение которых содержится в

.
Поскольку

и

- простой идеал, то один из идеалов

, ...,

содержится в

.
Без ограничения общности, предположим:

Поскольку

- простой идеал, то он является максимальным идеалом кольца

, поэтому

.
Если

, то из (2) следует:

, следовательно

, где

не является целым алгебраическим числом (иначе единица

принадлежала бы идеалу

, и

не был бы собственным идеалом).
Пусть

.
В силу минимальности

, произведение

не содержится в

.
Пусть

- целое алгебраическое число, принадлежащее

, но не принадлежащее

.
Тогда

, следовательно

, следовательно

.
Поскольку

, то

не принадлежит

и не является целым алгебраическим числом, что и требовалось.
Лемма
-------------
Пусть

- какой-либо ненулевой идеал кольца

.
Алгебраическое число

является целым алгебраическим числом тогда и только тогда, когда

cодержится в

.
Доказательство
------------------------
Если

- целое алгебраическое число, то

cодержится в

по определению идеала.
Пусть

- алгебраическое число, и

cодержится в

.
Докажем, что

- целое алгебраическое число.
Пусть

- абелева группа по сложению, генерируемая степенями

,

,

, ....
Пусть

- какой-либо ненулевой элемент идеала

.
Группа

содержится в идеале

, следовательно является подгруппой конечно-генерируемой абелевой группы.
Поэтому

, а значит и

является конечно-генерируемой абелевой группой.
Значит

- целое алгебраическое число.