Пусть

- конечное расширение полей.
Тогда любой элемент

поля

является алгебраическим над

.
В самом деле, поле

является подпространством над

конечно-мерного векторного пространства

над

, поэтому

является конечным расширением, следовательно элемент

является алгебраическим над

.
Полином с коэффиентами из поля

называется неприводимым над

, если он не разлагается в произведение полиномов ненулевой степени с коэффициентами из

.
Пусть

- конечное расширение полей.
Неприводимый над

полином

с корнем

называется минимальным полиномом элемента

.
Лемма
-------------
Пусть

- неприводимый над полем

полином степени

.
Тогда существует поле

, содержащее поле

, такое, что
![$[F:G]=n$ $[F:G]=n$](https://dxdy-01.korotkov.co.uk/f/8/3/0/830d9fc1bc80db2a86c48ab54843e9c082.png)
и полином

имеет корень в поле

.
Доказательство:
--------------------------
Если
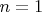
положим

.
Пусть

.
Пусть

- множество упорядоченных наборов, каждый из которых содержит

элементов поля

.
Каждому набору

из

поставим в соответствие полином

.
Пусть наборы

и

принадлежат

, и пусть

и

- соответствующие им полиномы.
Сумма

определяется как набор, соответствующий полиному

.
Пусть полином

является остатком от деления

на

в кольце полиномов с коэффициентами из поля

.
Определим произведение

как набор, соответствующий полиному

.
Множество

с этими операциями сложения и умножения является полем.
Пусть

- поле, полученное заменой в

каждого набора вида

элементом

.
Пусть

.
Тогда

и

.
Поскольку полином

неприводим над

, то
![$[F:G]=n$ $[F:G]=n$](https://dxdy-01.korotkov.co.uk/f/8/3/0/830d9fc1bc80db2a86c48ab54843e9c082.png)
.
Следствие 1
--------------------
Пусть

- полином с коэффициентами из поля

, степени

.
Тогда существует поле

в котором

имеет корень, и которое является конечным расширением поля

.
Доказательство
-------------------------
Пусть

- неприводимый над полем

полином ненулевой степени, который является делителем полинома

в кольце полиномов
![$G[x]$ $G[x]$](https://dxdy-04.korotkov.co.uk/f/7/c/5/7c5524818cae6f6bbcd58df4b84686fd82.png)
.
Согласно лемме,

имеет корень

в некотором поле

, являющимся конечным расширением поля

.
Элемент

является корнем полинома

.
Следствие 2
--------------------
Пусть

- полином с коэффициентами из поля

, степени

.
Тогда существует поле

в котором

разлагается на

линейных множителей, и которое является конечным расширением поля

.
Доказательство:
------------------------
Предположим обратное, и пусть

- наименьшая степень для которой это неверно.
Если
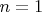
, то

разлагается на

линейных множителей в поле

, что противоречит предположению.
Пусть

.
Согласно следствию 1, существует поле
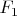
, в котором

имеет корень

, и которое является конечным расширением поля

.
Разделив полином

на

получим полином

с коэффициентами из поля
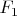
.
В силу минимальности

, существует поле

, в котором

разлагается на

линейных множителей, и которое является конечным расширением поля
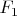
.
В поле

, полином

разлагается на

линейных множителей, и

- конечное расширение, что противоречит предположению.
Пусть

- конечное расширение полей.
Элемент

называется сепарабельным, если минимальный полином

, которому он принадлежит не имеет кратных корней ни в каком расширении поля

.
Если производная

не равна тождественно нулю, то

- не имеет кратных корней.
Это следует из того, что кратные корни

являются также корнями

и из неприводимости

.
Поэтому, если поле

имеет характеристику

, то

- не имеет кратных корней.
Расширение

называется сепарабельным, если все элементы поля

сепарабельны.
Все расширения, с которыми мы будем иметь дело, сепарабельны.
Несепарабельные расширения вообще редко встречаются (рекомендуем обсуждение сепарабельности в книге "Алгебра", Ван Дер Вардена).
Конечное расширение полей вида

называется простым расширением.
Теорема
--------------
Любое конечное сепарабельное расширение полей является простым.
Доказательство:
-------------------------
Пусть

- конечное сепарабельное расширение полей.
Тогда

, где

, ...,

- базис этого расширения.
Докажем, что расширение

является простым для любых элементов

поля

.
Предположим обратное, и пусть

- наименьшее целое положительное число, для которого это не верно.
Если

, то расширение

- простое, что противоречит предположению.
Пусть

.
В силу минимальности

, расширение

является простым.
Значит существует такое

, что

.
Пусть

.
Докажем, что

- простое расширение.
Поскольку

- конечное расширение, то элементы

и

являются алгебраическими над

.
Пусть

- минимальный полином элемента

, и

- минимальный полином элемента

.
Согласно следствию 2, существует поле

, содержащее поле

, и такое, что полиномы

и

разлагаются в

на линейные множители.
Пусть

, ...,
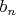
- все корни полинома

(

), принадлежащие

.
Пусть

, ...,

- все корни полинома

(

), принадлежащие

.
Пусть

, где

будет выбран позднее.
Имеем:

и

.
Выберем

так, чтобы полиномы

и

имели в поле

единственный общий корень

.
Условия этого:

, при

;

.
Или

, или
(1)

, при

;

.
Поскольку элемент

принадлежит

, и

является сепарабельным расширением, то

является сепарабельным элементом.
Поэтому

при

, и существует

, удовлетворяющее условиям (1).
Из того, что полиномы

и

имеют в поле

единственный общий корень

,
следует, что

является наибольшим общим делителем этих многочленов.
Поскольку все коэффициенты этих многочленов принадлежат полю

, то

.
Теперь из

следует

.
Значит

, а поскольку

, то расширение

является простым, что противоречит предположению.
Алгебраическими числами, называются комплексные числа, алгебраические над полем рациональных чисел

.
Пусть

и

- алгебраические числа.
Тогда
(1)
![$[\mathbb{Q}(a, b):\mathbb{Q}]=[\mathbb{Q}(a, b):\mathbb{Q}(a)][\mathbb{Q}(a):\mathbb{Q}]$ $[\mathbb{Q}(a, b):\mathbb{Q}]=[\mathbb{Q}(a, b):\mathbb{Q}(a)][\mathbb{Q}(a):\mathbb{Q}]$](https://dxdy-03.korotkov.co.uk/f/a/3/7/a37ad7a3b0c1e0adc9c581567e28c2d482.png)
.
Поскольку число

- алгебраическое над

, то оно тем более алгебраическое над

, поэтому сомножители в правой части (1) конечны, следовательно

является конечным расширением полей.
Поскольку

,
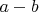
,

и

(при

) принадлежат полю

, то эти числа являются алгебраическими.
Таким образом множество всех алгебраических чисел является полем.
Поле всех алгебраических чисел не является конечным расширением

, и оно не так интересно для нас, как его подполя

, для которых

является конечным расширением.
Подполе

поля всех комплексных чисел называется числовым полем, если

является конечным расширением.
Все элементы числового поля являются алгебраическими числами.
Если

- числовое поле, то расширение

является простым, значит существует алгебраическое число

, такое что

.