.
.
.
.
.
.
.
.
.
Докажем, что это верно и в том случае, если группа

не является абелевой.
Центром группы называется множество элементов, коммутирующих со всеми её элементами.
Если

принадлежит центру, то

тоже ему принадлежит.
Если

и

принадлежат центру, то

тоже ему принадлежит.
Поэтому центр группы

является подгруппой (и даже нормальной подгруппой).
Пусть

- какой-либо элемент группы

.
Нормализатором элемента

называется множество всех элементов группы

, коммутирующих с

.
Нормализатор элемента

является подгруппой группы

и обозначается через

.
Если

, то

и

находятся в одном правом смежном классе нормализатора

(поскольку

).
Поэтому колличество различных элементов вида

равно колличеству правых смежных классов нормализатора

.
Пусть

конечная группа, порядок которой делится на простое число

.
Пусть

наибольшая степень

, на которую делится порядок группы

.
Тогда в

существует подгруппа порядка

.
Чтобы доказать это предположим обратное и пусть

группа наименьшего порядка, такая что
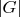
делится на

, не делится на

(где

- целое положительное число), и в

не существует подгруппы порядка

.
Обозначим центр группы

через

.
Докажем, что порядок

не делится на

.
Предположим обратное, тогда в

существует подгруппа порядка

.
Обозначим эту подгруппу через

.
В силу минимальности порядка

, фактор-группа

содержит подгруппу порядка

.
Элементами этой подгруппы являются смежные классы, объединение которых является подгруппой (группы

), порядка

.
Это противоречит тому, что такой подгруппы не существует.
Введём отношение

, если

, для некоторого элемента

группы

.
Это отношение является отношением эквивалентности и разбивает

на непересекающиеся классы

,

, ...,

.
Обозначим колличество элементов в

через

.
Докажем, что если

для какого-то j, то

делится на

.
Предположим обратное, что

не делится на

.
Тогда порядок нормализатора любого элемента, принадлежащего

делится на

, поскольку

равно колличеству правых смежных классов этого нормализатора.
В силу минимальности порядка

, в этом нормализаторе есть подгруппа порядка

, что невозможно, поскольку в

нет такой подгруппы.
Из доказанного и равенства

следует, что колличество

содержащих по одному элементу делится на

.
Это колличество равно порядку центра группы

, в противоречии с тем, что порядок этого центра не делится

.



