Представляю обещанный анализ процедуры P1.
Первая же фраза в описании алгоритма вызывает недоумение:
Цитата:
Let graphs G,G′ are isomorphic.
Означает ли это, что данный алгоритм проверки изоморфизма к не изоморфным графам не применим?
Означает ли это, что нам нужен ещё один алгоритм проверки изоморфизма графов, чтобы решить вопрос можно ли применять данный алгоритм проверки изоморфизма графов?
Нонсенс.
Мысленно заменим "изоморфные" на "простые связные" и продолжим наш анализ.
Пусть

означает отсортированную в неубывающем порядке

-ю строку матрицы

Очевидно, что вектор

является инвариантом подобия, то есть если вершины

и

подобны, то вектора

и

равны.
Пусть

означает матрицу

каждая строка которой отсортирована в неубывающем порядка, а затем сами строки отсортированы в лексикографическом порядке.
Очевидно, что матрица

является инвариантом графа, то есть если графы

и

изоморфны, то матрицы

и

равны.
Допустим, что процедуре P1 работает правильно. Тогда она проверяет подобна ли вершина

графа

вершине

графа

И если они подобны, то выдаёт изморфизм

графа

на граф

такой, что

А если не подобны выдаёт пустое множество.
Исходя из этого, мы можем, без всякой потери общности, ограничиться рассмотрением только таких графов

и

для которых

Пусть

и

означает разбиение множества

и

, соответственно, на классы псевдоподобных вершин, индуцированное инвариантом подобия

То есть вершины

и

графа

принадлежат одному классу псевдоподобия, если и только если

Так как

, то разбиения

и

аналогичны. В том смысле, что имеют одинаковое число классов псевдоподобия, одинаковые наборы инвариантов подобия, и одинаковые мощности соответствующих классов (с равными

).
Пусть

означает разбиение

у которого вершина

индивидуализирована, то есть выделена в отдельный класс единичной мощности.
Построим двудольный граф

, где

множество вершин графа

,

множество вершин графа

,

множество рёбер графа

, такое что вершина

соединена с вершиной

, если и только если

Пусть

означает граф

в котором вершины

и

индивидуализированы, то есть выделены в отдельные классы единичной мощности, а из всех рёбер, инцидентных данным вершинам, оставлено только ребро

Выберем вершину

и вершину

Без потери общности можно считать, что

В противном случае вершины

и

не подобны, и правильно работающая процедура P1 выдаст пустое множество.
Вектор

определяет разбиение

множества

, объединяя в один класс такие вершины

, что

Аналогично вектор

определяет разбиение

множества

, условием -- вершины

принадлежат одному классу разбиения

тогда и только тогда, когда

Очевидно, что разбиение

является более грубым по сравнению с разбиением

. То есть один класс разбиения

может состоять из нескольких классов разбиения

. Аналогично разбиение

является более грубым по сравнению с разбиением

Так как

, то разбиение

аналогично разбиению

, в том смысле что у них совпадает число классов, множество различных элементов вектора

совпадает с множеством различных элементов вектора

, и равны мощности соответствующих классов.
Выполним шаг 1) процедуры P1, то есть построим двудольный граф

по правилам описанным в статье.
Очевидно, что множество

рёбер графа

является подмножеством множества
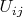
рёбер графа

Приступим к выполнению шага 2) процедуры Р1.
На этом шаге выполняется цикл по всем рёбрам графа

(фактически итерации будут выполняться только по тем рёбрам которые ещё небыли удалены на предыдущих итерациях).
Так как порядок выбора рёбер не указан, то можем выбрать любой.
Поэтому разобьём шаг 2) на два этапа:
на первом выбираем рёбра принадлежащие множеству 
на втором принадлежащие множеству  .
.
То есть на первом этапе будут проверяться рёбра соединяющие заведомо не подобные вершины, так как их инварианты подобия

различны.
Правильно работающая процедура Р1 будет такие рёбра из исходного графа

удалять.
Таким образом по окончании первого этапа наш граф

будет совпадать с графом

.
То есть уже на 1) шаге процедуры Р1 мы можем вместо графа

взять граф

, без всякой потери общности.
Замечаем, что на втором этапе шага 2) процедуры Р1 выполняется условие

Поэтому и на шаге 2) процедуры Р1 мы можем вместо графов

использовать графы

, без всякой потери общности.
Замечаем, что на втором этапе шага 2) процедуры Р1 функция Т() всегда находит трансверсаль. То есть по окончании шага 2) мы получим некоторую трансверсаль которая, как мы надеемся, представляет изоморфизм графа

на граф

На шаге 3) найденный "изоморфизм" выдаётся на-гора.
Видим, что процедура Р1 фактически работает не с графом

, а с разбиениями

и

Её можно записать так:
1) на входе получаем псевдоподобные вершины

и

(то есть

)
2) для каждой индивидуализированной вершины

разбиения

(то есть вершины принадлежащей классу псевдоподобия единичной мощности) добавляем к изначально пустому отображению

пару

, где

-- вершина разбиения

соответствующая вершине

(такая вершина обязательно имеется, причём ровно одна, так как разбиение

аналогично разбиению

)
3) если вершины

и

ещё не индивидуализированы, то индивидуализируем их и добавляем к отображению

пару

4) если все вершины разбиения

уже индивидуализированы, то выдаём отображение

и останавливаемся
5) выбираем не индивидуализированную вершину

разбиения

выбираем не индивидуализированную вершину

из класс псевдоподобия разбиения

, соответствующего классу псевдоподобия вершины

добавляем к отображению

пару

6) если разбиение

имеет ещё не обработанные индивидуализированные вершины (одна такая вершина может появиться на предыдущем шаге когда мощность класса псевдоподобия вершины

равна двум), то соответствующие пары добавляем к отображению

7) возвращаемся на шаг 4).
Это очень плохой алгоритм.
Ранее в этой теме он уже разбирался и был отвергнут.
Именно для замены этого алгоритма Вами был предложен
Алгоритм 1, который работает абсолютно правильно на графах у которых разбиение

множества вершин на классы псевдоподобия совпадает с автоморфным разбиением.
Вот его-то (Алгоритм 1) и нужно использовать в процедуре Р1.
Ваш подход к решению проблемы изоморфизма графов безусловно заслуживает самого пристального внимания. И хотя класс графов на которых он применим, по всей видимости, очень и очень широк, всё же он не охватывает класса всех графов.
Свои аргументы изложу в следующий раз, а то пост и так получился слишком большим.