Найдите радиус

окружности, вписанной в равносторонний треугольник со стороной

и радиус

окружности, описанной около него.

Прошу прощения за чертёж, далёкий от идеала.
Пусть

- центр обеих окружностей.

- равносторонний тр-к со стороной

. Т.

- срединная т.

. Т. о.

.
Тр-к
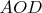
- прямоугольный, т. к.

лежит на медиане и высоте

и, следовательно, перпендикулярен

C.
Проведём отрезок

. По Теореме центр вписанной в тр-к окружности есть точка пересечения его биссектрис.
Следовательно,

- биссектриса, а угол



, т. к.


.


Следовательно,









Таким образом, получил следующее:

;

Но с ответами это не сходится. Не могу понять, в чём допущена ошибка.



