Munin.Это безосновательное заявление было сделано еще Фейнманом.
У Фейнмана, как раз точно такая формула и используется при выводе соотношения неопределенностей, для получения равенства
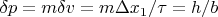
стр.65.
Ничего обратного тому что я сказал, Фейнман не утверждает. Напротив его формула 3.28
![$P(x,\tau ) dx =(m/2(\pi) hT\Delta{x})exp[-(x-v\tau)^{2}/( \Delta{x} ) ^{2}]dx$ $P(x,\tau ) dx =(m/2(\pi) hT\Delta{x})exp[-(x-v\tau)^{2}/( \Delta{x} ) ^{2}]dx$](https://dxdy-02.korotkov.co.uk/f/5/4/1/54141100c8b7175e7b982c161c18ade482.png)
говорит о том, что наиболее вероятная траектория это прямая
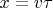
. Чтобы показать противоречивость стандартной Боровской интерпретации соотношения Гейзенберга, достаточно рассматриваеть только эту единственную траекторию.

Разумеется траехтории могут быть любыми, но классическая траехтория
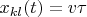
как раз и есть наиболее вероятная.



Для произвольной траехтории
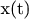
, нужно пользоваться средней скоростью
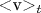
частицы на траехтории
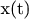
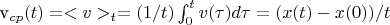
.
Для средней скорости,в случае примера измерения координаты, который описан у Фейнмана на стр60-64,соотношение неопределенностей, имеет вид
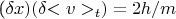
.
Отсюда получается такое же противоречие с канонической Боровской интерпретацией СН,
без предположения, что траектория прямая.

Теория вероятностей и теория случайных процессов, это две совершенно разные вещи.
Теория марковских процессов с комплексной амплитудой перехода, построена 30 лет назад
в работах Маслова. Маслов как раз и взял за основу, эвристическую конструкцию Фейнмана,
которая для свободной частицы, является математически корректной, потому что интеграл
гауссовский и вычисляется в явном виде.С современным состоянием теории можно ознакомиться здесь
http://arxiv.org/abs/quant-ph/0205132
Quantum processes on phase space
Authors: Charis Anastopoulos
Comments: 53 pages, latex. Minor corrections - final version to appear in Ann. Phys
Journal-ref: Annals Phys. 303 (2003) 275-320
Quantum theory predicts probabilities as well as relative phases between different alternatives of the system. A unified description of both probabilities and phases comes through a generalisation of the notion of a density matrix for histories; this object is the decoherence functional of the consistent histories approach. If we take phases as well as probabilities as primitive elements of our theory, we abandon Kolmogorov probability and can describe quantum theory in terms of fundamental commutative observables, without being obstructed by Bell's and related theorems. Generalising the theory of stochastic processes, we develop the description of relative phases and probabilities for paths on the classical phase space. This description provides a theory of quantum processes. We identify a number of basic postulates and study its corresponding properties. We strongly emphasise the notion of conditioning and are able to write ``quantum differential equations'' as analogous to stochastic differential equations. These can be interpreted as referring to individual systems. We, then, show the sense in which quantum theory is equivalent to a quantum process on phase space (using coherent states). Conversely, starting from quantum processes on phase space we recover standard quantum theory on Hilbert space from the requirement that the process satisfies (the Markov property together with time reversibility. The statistical predictions of our theory are identical to the ones of standard quantum theory, but the ``logic'' of events is Boolean; events are not represented by projectors any more. We discuss some implication of this fact for the interpretation of quantum theory, emphasising that it makes plausible the existence of realist theories for individual quantum systems.