годограф Михайлова

[Sverest]

нашел такой пример:
Вид годографа Михайлова неустойчивой системы шестого порядка:
$F(p)=p^6+9p^5+17p^4+120p^3+62p^2+300p+100$

$F(j\omega)=100-62\omega^2+17\omega^4-\omega^6+j(9\omega^5-120\omega^3+300\omega)$



Не разобрался как строится годограф
Вижу первую точку $P(\omega)=100$, но почему при этом $Q(\omega)=0$ ?

[spctr]

Подумайте, что такое $P(\omega)$ и $Q(\omega)$, чему они равны в данном случае и чему равна $\omega$ в начальной точке.

[Sverest]

это прямые действительных и комплексных чисел $a+bj$

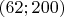
откуда взялась точка $(62;200)$? ведь нет комплексного $200$

из другого примера понял, что просто берутся значения $\omega$ и подставляются в формулу $F(j\omega)=100-62\omega^2+17\omega^4-\omega^6+j(9\omega^5-120\omega^3+300\omega)$, получается комплексное число, оно отмечается на годографе

значения $\omega$ брать любые?