Подобные призмы в многомерном пространстве

[Nikolai Moskvitin]

N-призмой называются два $(N-1)$-многогранника, которые лежат в двух параллельных $(N-1)$-плоскостях, через все соответственные $K-грани$ которых проведены $(K+1)$-плоскости.
Цель сообщения- прошу помочь доказать предположение, данное ниже.

Вначале я ввёл понятие главной диагонали:
Главная диагональ [b]N-призмы, у которой все 2-мерные грани-параллелограммы -отрезок, соединяющий любую вершину призмы и точку, не принадлежащую ни одной из гиперплоскостей размерности меньше, чем N (в том числе размерности (N-1)), проходящих через эту вершину. Назовём такую точку «изолированной» и обозначим её D. (Гиперплоскость называется проходящей через точку, если последняя принадлежит ей.)
Пусть теперь даны две подобные N-призмы, расположенные в пространстве так, что они имеют общую вершину (C) и ровно n общих прямых, проходящих через неё, причём только для одной из них две вершины этих призм лежат по разную сторону от C (A и B).[/b]
Тогда я делаю следующее предположение:
Середина отрезка, соединяющего концы главных диагоналей, не являющихся общими, соответственно меньшей и большей призм,проведённых из точки C, лежит на главной диагонали второй, проведённой из точки $B$, и на продолжении главной диагонали первой, проведённой из точки $A$. При этом$ AC<BC$.

Докажем сначала в 2-мерном пространстве.
Условие: на отрезке $AG$ взята произвольная точка $D$ (пусть для определённости $AD <DG$) и на полученных отрезках как на основаниях построены параллелограммы $ABCD$ и $DEFG$, подобные друг другу, с вершинами по одну сторону от отрезка $AG$ и точками $D,C,E $на одной прямой.
Доказать: середина отрезка $BF$ лежит на диагонали одного параллелограмма и на продолжении диагонали другого.

Пусть $L$- исследуемая середина. Проведём через $L$ прямые, параллельные $AB$ и $FG$ и $EF$ и $AG$ соответственно. Пусть первая из них пересекает сторону $DG$ в точке $K$, а вторая- $FG$ в точке $M$. Обозначим стороны $AB$,$AD$ и $DE$,$DG$ параллелограммов ABCD и DEFG как a,b и c,d соответственно. $AK=KG $по теореме Фалеса. Поэтому $LM=\frac{b+d}{2}$, т.к.$ LM=KG$. Также и$ LK=\frac{a+c}{2} $(по теореме о средней линии трапеции). Докажем, что параллелограммы KLMG и DEFG подобны. Тогда ясно, что поскольку у них общий угол, их диагонали LG и EG лежат на одной прямой (по различным свойствам подобия), откуда следует утверждение задачи. По условию $a:b=c:d $ Докажем, что$ a:b=(a+c):(b+d)$. $ab+ad=ab+bc$, но $ad=bc$, поэтому это утверждение верно. Следовательно, доказано подобие параллелограммов $KLMG$ и $DEFG$, а значит и утверждение задачи. Для меньшего параллелограмма утверждение доказывается аналогично.

Докажем теперь, что из одной вершины выходит только одна главная диагональ. Для этого используем контрпример. Сначала возьмём двумерное пространство и фигуру в нём-отрезок. Если на нём построить параллелограмм, две стороны последнего будут пересекаться в одном из его концов и будут содержать все его вершины, кроме одной. По нашему определению получается существование только одной главной диагонали (см. выше) из данной вершины для 2-мерного пространства. Если теперь на параллелограмме как на основании построить параллелепипед, оставшаяся вершина параллелограмма окажется на 2-плоскости, проходящей через искомый конец (ей будут принадлежать две пересекающиеся прямые по аксиоме 2(см.тетрадь), а значит, и точка пересечения), аналогично вершины двух других параллелограммов окажутся на 2-плоскостях, проходящих через этот конец, и только одна точка окажется изолированной. Применяя аналогичное рассуждение, получим, что при дальнейшем увеличении числа измерений изолированная точка будет одна, а следовательно, главная диагональ, выходящая из данной вершины, одна.
Пусть призма, образованная прямыми большей призмы, проходящими через $B$, и прямыми, выходящими из исследуемой точки (обозначим её $L_n$ в зависимости от числа измерений, для которого она исследуется) и параллельными рёбрам обеих призм, обозначим X.
Пусть различные рёбра призмы $X$ равны $a_1,a_2,...a_n$, различные рёбра меньшей данной призмы- $b_1,b_2...b_n$, большей- $с_1,с_2...с_n$.
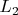
Чтобы не выглядеть бездоказательным, докажу пока только для трёх мерного пространства. Соответственно ${n}={1,2,3} $. Обозначим призмы $ABCDEFGH$ и$ DIJKLMNP$ (согласно правилам первые четыре буквы обозначают нижнее основание, вторые четыре-верхнее). Проведём через$ L_2$ прямые, параллельные $CD$ и $DK$ (пусть они пересекают $DK$ и $JK$ соответственно в точках $R$ и $S$).
Тогда $\frac{KL_2}{KI}={\frac{L_2S}{IJ}}$, но $\frac{L_2S}{IJ}={\frac{AD}{DK}}={\frac{AE}{LN}}$, а значит, $\frac{L_3L_2}{IM}={\frac{KL_2}{KI}}$, отсюда следует утверждение задачи для 3-х мерного пространства.

Жду дальнейших замечаний, с уважением, Николай

[Утундрий]

Двенадцать лет назад Я сформулировал Всеобщую Теорию Всего (Этой идее 102 года) частным случаем которой являются эти Ваши... Ну, эти Ваши... как же их... А, да - N-призмы! Но поскольку Время - идёт, и всего не упомнишь (Всё моё внимание нынче поглощает Новейшая Теория Ничего) то почему бы Вам не начать свой доклад с определения этих Ваших... ну, этих Ваших... ну, Вы поняли!

[zhoraster]

Но начнем мы не с определения, а с Карантина.
- сформулируйте по возможности кратко и четко предмет обсуждения;
- наберите формулы надо набирать в нотации $\TeX$. Как это делать, можно посмотреть в теме Краткий ФАК по тегу [math].

Исправьте все свои ошибки и сообщите об этом в теме Сообщение в карантине исправлено.

Также в качестве полезного чтения рекомендую Правила научного форума.

[zhoraster]

Возвращено.

[Утундрий]

Nikolai Moskvitin в сообщении #571984 писал(а):

(см.тетрадь)

Не волне очевидно, как сие действо произвести.

[Nikolai Moskvitin]

Утундрий в сообщении #574387 писал(а):

Nikolai Moskvitin в сообщении #571984 писал(а):

(см.тетрадь)

Не волне очевидно, как сие действо произвести.

Тогда см. учебник по геометрии за 10 класс. :)
Попробую всё же начать доказывать.

1)Пусть отрезок, середину которого мы исследуем- $EF$, сама середина- $L_n$. Возьмём в качестве леммы следующее утверждение: длины параллельных рёбер N-призмы, у которой все грани-параллелограммы, равны. Из леммы следует, что безразлично, на какую гиперплоскость в целях доказательства проектировать точку $L_n$, лишь бы соблюдалось одно ограничение, о котором сейчас будет сказано. Проведём через$ L_n$ прямую, параллельную любым параллельным рёбрам, содержащим E и F, но с одним ограничением: вторые их концы не принадлежат гиперплоскости размерности $N-1$, проходящей через грани этой же размерности, одна из которых целиком принадлежит другой (по условию таких граней всегда будет пара). Назовём такие рёбра «подходящими». Обозначим вторые концы подходящих рёбер (отличные от E и F) как $E_1$ и $F_1$.

2)Проведём через все три полученные параллели 2-плоскость.(По теореме, $L_n$ принадлежит плоскости этих рёбер, значит, ей принадлежит и построенная параллель). Пусть проекция $L_n$ на гиперплоскость размерности $N-1$, содержащую основания N-призм, которым принадлежат $E_1$ и$ F_1$ -$L_{n-1}$ (направление проектирования задаётся построенными параллелями). Тогда длина отрезка $L_nL_{n-1}$ будет равна полусумме рёбер $EE_1$ и $FF_1$(по теореме о средней линии трапеции).

Пока остановлюсь. Как вообще должно выглядеть доказательство утверждения для многомерного пространства? Несомненно, термины (гиперплоскость, и т.п.). Но мне нужен образец такого доказательства (без вычислений).

[Nikolai Moskvitin]

Продолжим доказательство:

3)Преобразование проекции переводит точки в гиперплоскость меньшей размерности (на один), поэтому продолжим проектировать проекции точки L по следующему правилу: выбираем на любой паре подходящих рёбер с концами $E_n $и $F_n$ вторые концы ($E_{n+1}$ и $F_{n+1}$), и на гиперплоскости размерности $(N-2)$, проведённой через основания $(N-1)$-призм, содержащие $E_{n+1}$ и $F_{n+1}$, строится проекция точки $L_n$ на эту гиперплоскость- $L_{n+1}$ (направлением проекции являются рёбра $E_nE_{n+1}$ и $F_nF_{n+1}$). Дойдём так до второго измерения, в котором теорема уже доказана. Тогда длины всех отрезков вида $L_nL_{n+1}$ будут равны полусумме параллельных им рёбер соответственно большей и меньшей призм, принадлежащих одной с ними 2-плоскости.

4)Построим теперь N-призму, опустив из точки P параллели (её рёбра) на все гиперплоскости большой призмы, для которых она является изолированной так, чтобы эта призма имела все те общие гиперплоскости с большой призмой, которые проходят через точку B. (размерность их- N-1). Тогда по доказательству все её рёбра, исходящие из точки P, будут равны полусумме соответствующих рёбер искомых призм, лежащих с ними в одной 2-плоскости.
Докажем, что полученная призма будет подобна искомым. Для этого можно для каждой пары непараллельных рёбер доказать, что они относятся друг к другу также, как и аналогичная пара рёбер каждой из искомых призм. Поскольку все такие соотношения симметричны (т.е. доказательство не зависит от выбора пары рёбер: все такие пары состоят из отрезков, находящихся по утверждению задачи в одном и том же соотношении) , можно доказать это для одной пары рёбер. Но поскольку мы уже имеем подобное доказательство для двумерного пространства, подобие выполняется.

Прошу всё-таки помочь мне исправить ошибки, скорее неточности, если они есть. Тогда продолжу доказательство.

С уважением, Николай