пусть

аналитична в области

включающей единичный круг {

}

для всех

и

доказать, что существует

так что
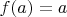
что-то похожее решали на лекции. но там мы доказывали, с помощью принципа максимума, что существует ноль у функции и, по моему, там было условие непрерывности на границе области.
какую теорему здесь использовать? доказывать от противного?
заранее спасибо