Извиняюсь, что отвлёкся от разговора. В такую прекрасную погоду больше хочется играть джаз, чем думать о математике:)
Цитата:
У меня такой "интуиции" нет. Просто я знаю, что существование функции с каким-то свойством зависит от того, какое именно это свойство. Почему свойство "быть функцией выбора" кажется Вам таким уж легко выполнимым, мне непонятно.
Попытаюсь объяснить...хотя это ощущение скорее иррациональное. В общем, если мыслить аналогиями с всеми функциями вида
![$[0,1]\to[0,1]$ $[0,1]\to[0,1]$](https://dxdy-04.korotkov.co.uk/f/3/d/0/3d0c9dd39cf34aece547edb03d0f26c682.png)
(да, спасибо за поправку, вот теперь "просто" гиперконтинуум), то интуиция подталкивает к тому, что множество таких функций - суть множество неких трансфинитных последовательностей (ещё раз, мы говорим об интуиции) И тут начинает включаться аналогия с последовательностями "обычными". В таком ракурсе можно говорить так: "функция такая-то и такая-то есть, так как это просто очередная последовательность". Но почему-то я стороной обходил тот факт, что в первую очередь ещё нужно доказать то, что, собственно, эта "функция" является одной из таких последовательностей в принципе, а интуиция никак не хотела подкинуть соответствующий примерчик из множества
![$[0,1]\to[0,1]$ $[0,1]\to[0,1]$](https://dxdy-04.korotkov.co.uk/f/3/d/0/3d0c9dd39cf34aece547edb03d0f26c682.png)
. Например, вопрос о существовании разрывной функции вида

, существование которой, собственно, из аксиомы выбора и вытекает. Видимо, надо было просто сконцентрировать внимание на этом вопросе.
Цитата:
Что значит - "любой элемент"? Если Вы думаете, что Ваше "определение" что-нибудь определяет, то Вы ошибаетесь. Когда мы говорим, что задано отображение

, то

- это вовсе не "любой" элемент, это некоторый вполне определённый элемент для каждого

. Если Вы хотите определить отображение, Вы должны для каждого

указать совершенно конкретный элемент

. Когда укажете, тогда можно будет говорить об отображении.
Огромное Вам спасибо!
Цитата:
О, боже! Взяли бы список аксиом ZFC и посмотрели. Например, в книге К.Куратовского и А.Мостовского "Теория множеств".
Пустое множество

существует по аксиоме существования пустого множества.
Неупорядоченная пара

существует по аксиоме пары.
Объединение множеств
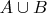
существует по аксиоме суммы.
Множество подмножеств

существует по аксиоме степени.
Множество

(и, в частности,

) существует по аксиоме выделения.
Если

и

, то неупорядоченная пара

является элементом множества

.
Существование упорядоченной пары

, если её определить как

, следует из существования неупорядоченной пары.
Упорядоченная пара

, где

и

, является элементом множества

, поэтому произведение

, определяемое как множество упорядоченных пар

, где

и

, существует по аксиоме выделения.
Отображение

, с точки зрения теории множеств, есть подмножество произведения

, удовлетворяющее некоторому условию, поэтому множество

отображений

существует по аксиоме выделения.
Да, всё ясно, как божий день, спасибо, ещё раз!
Теперь я и понял суть леммы Цорна и всю её неочевидность. Всё, что нужно для перехода от неё к аксиоме выбора - показать непустое множество, состоящее из систем подмножеств, на которых мы можем определить функцию выбора (достаточно одноэлементных множеств), затем показать то, что любая цепь таких функций также ограничена и, вуаааля, волшебным образом мы получим существование максимального элемента! Теперь только остаётся доказать, что, в частности, он совпадает со всем множеством
![$P([0, 1])\to[0, 1]$ $P([0, 1])\to[0, 1]$](https://dxdy-01.korotkov.co.uk/f/c/0/9/c0981fab0b7c61622070688dc7c813d282.png)
и "теорема" выбора доказана! Чудеса аксиоматики!
Озарение пришло, вы мне очень помогли.



