Призма в сфере

[Алексей К.]

(Оффтоп)

Алексей К. в сообщении #559410 писал(а):

И никто из умных и отзывчивых их не подсказывает

Явились, наконец... На третий день...

[ewert]

gris в сообщении #559559 писал(а):

А числовая часть неравенства чудом совпадает с заданным объёмом

Не совсем чудом. Чтобы задача имела единственное решение в случае "общего положения", надо, чтобы площадь была однозначной функцией объёма, а это очевидно неверно. Следовательно, если задача корректна, то это должен быть какой-то экстремальный случай. И поскольку фиксирован объём -- напрашивается проверка, не является ли именно данное значение объёма экстремальным.

[gris]

Там у чуда вроде бы "кавычки" стояли. Наверное, модератор стёр.
Написал было методические рассуждения, но не буду флудить.
Короче, я что хотел сказать. Что увидев постоянную сумму переменных величин школьнику полезно сразу применить к ней известное неравенство, тем более, что произведение сторон явно напрашивается.
Что должно всплыть в голове: вписанный параллелепипед — прямоугольный — диагональ равна диаметру — суммы квадратов сторон — произведение сторон — неравенство.

[ewert]

(Оффтоп)

gris в сообщении #559582 писал(а):

Что должно всплыть в голове: вписанный параллелепипед — прямоугольный — диагональ равна диаметру — суммы квадратов сторон — произведение сторон — неравенство.

Ну можно, конечно; но зачем, если геометрически и так всё очевидно.

[Keter]

gris в сообщении #559559 писал(а):

Не знаю, было ли это уже в обсуждении, но намёки явно были.
У нас фиксирована сумма квадратов сторон, что необходимо и достаточно (вкупе с прямоугольностью) для вписания параллелепипеда. Для тех же квадратов можно выписать неравенство между средним арифметическим и средним геометрическим. Получим нестрогое неравенство для объёма, которое превращается в равенство только при равенстве ингредиентов. А числовая часть неравенства чудом совпадает с заданным объёмом. Получаем искомый куб.

Я писал в первом же сообщении неравенство Коши, а оно аналогично тому, что Вы привели. Один вопрос - а можно разве говорить о том, что у нас обязательно должно быть равенство?

[Keter]

gris в сообщении #559559 писал(а):

Не знаю, было ли это уже в обсуждении, но намёки явно были.
У нас фиксирована сумма квадратов сторон, что необходимо и достаточно (вкупе с прямоугольностью) для вписания параллелепипеда. Для тех же квадратов можно выписать неравенство между средним арифметическим и средним геометрическим. Получим нестрогое неравенство для объёма, которое превращается в равенство только при равенстве ингредиентов. А числовая часть неравенства чудом совпадает с заданным объёмом. Получаем искомый куб.

Я писал в первом же сообщении неравенство Коши, а оно аналогично тому, что Вы привели.

Теперь я понял:

1)если решать задачу на максимум-минимум методом неравенств, то используем неравенство Коши:

Из диагонального сечения мы выяснили, что $a^2+b^2+c^2 = 12$, теперь Коши

$\frac{a_1+a_2+...+a_n}{n} \geqslant \sqrt[n]{a_1 \cdot a_2 \cdot ... \cdot a_n}$

$\frac{a^2+b^2+c^2}{3} \geqslant \sqrt[3]{a^2 \cdot b^2 \cdot c^2}$

Следствием из Коши является то, что произведение неотрицательных сомножителей, сумма которых постоянна, принимает наибольшее значение, когда все эти сомножители равны $(a = b = c)$. То есть максимальное значение $a^2 \cdot b^2 \cdot c^2 = a^6 = 64; a = 2; abc = a^3 = 8$. Итак, максимальный объём данного параллелепипеда 8, то есть данный. А так как это возможно только при условии, что $(a = b = c)$, то он является кубом.

2)

Алексей К. в сообщении #559548 писал(а):

"В заданную окружность радиуса $R$ вписать прямоугольник максимальной площади"

Обозначим через $R$ радиус круга, а через $x$ сторону АВ искомого прямоугольника.
По теореме Пифагора $BC = \sqrt{4R^2-x^2}$.

$S = x \sqrt{4R^2-x^2}$

Эта функция достигает своего наибольшего значения при том же самом $x$, что и функция $f(x) = S^2$.

$f(x)=x^2 (4R^2-x^2)$

Пусть $x^2=t$ получим:

$f(t)=t(4R^2-t)=-t^2+4R^2 t$

Значит $\max E(f)$ достигается при $t=2R^2$,т.е. при $x = R \sqrt2$.

Ну а при $AB=x= R \sqrt2, BC=R \sqrt2$ искомый прямоугольник должен быть квадратом.

[Алексей К.]

Keter,

трудности в общении с Вами у меня (как часто бывает на форуме), проистекают от того, что общаемся мы письменно, что не есть эффективно.
С одной стороны, Вы демонстрируете совершеннейший дилетантизм: в первую очередь, это было то самое "деление неравенств", а также Ваша реакция на некоторые вопросы.
С другой стороны оказывается, что Вы совсем не так плохо разбираетесь в математике; Ваше решение задачки про квадрат правильно и хорошо расписано. Грамотно, приятно читать. Я хотел производные забабахать, другие другое предлагали, Вы же опёрлись на свойства квадратичной функции. И, повторяю, здорово всё изложили.
(Вы один и тот же человек? )

Я сегодня не могу активно участвовать, почитаю и продолжу завтра. Мне показалось, что трёхмерную задачу Вы уже тоже обосновали в Вашем предыдущем сообщении. Не хватает только упоминаний (подчёркиваний) единственности найденных решений.

И вообще --- у нас остались неясности? Может, Вы изложите свою окончательную (краткую) версию решения? Ну, Ваши последние обращения к отношениям объёмов были очень уж подозрительны, совсем ни к чему...

[Keter]

Цитата:

трудности в общении с Вами у меня (как часто бывает на форуме), проистекают от того, что общаемся мы письменно, что не есть эффективно.

Полностью согласен.

Цитата:

Вы демонстрируете совершеннейший дилетантизм: в первую очередь, это было то самое "деление неравенств", а также Ваша реакция на некоторые вопросы.

Вчера был очень сложный день. Не очень хорошо думалось. Вот я и "поделил"((

Цитата:

оказывается, что Вы совсем не так плохо разбираетесь в математике

Спасибо.

Цитата:

Вы один и тот же человек?

Немного расскажу о своей проблеме. В основном я изучал математику сам, что касается олимпиадных задач. И у меня нет как бы наработки в их разных типах. Поэтому когда я беру какую то задачу, то приходится понимать некоторые моменты с нуля, а она оказывается типовой. Вот например задачи на максимум-минимум я никогда не решал. Пришлось придумывать решение.

-- 13.04.2012, 23:51 --

В сферу с радиусом $R = \sqrt{3}$ вписан параллелепипед, объём которого $V = 8.$ Найти площадь полной поверхности параллелепипеда.

1)Обозначим длину, ширину и высоту параллелепипеда соответственно $a, b, c$.

2)Диагональным сечением параллелепипеда будет прямоугольник со сторонами $c$ и $\sqrt{a^2+b^2}$ и диагональю $2\sqrt{3}$.

По теореме Пифагора $a^2+b^2+c^2 =12$.

3)Объём данного параллелепипеда $V = abc = 8$.

Найдём параллелепипед максимально возможного объёма, который можно вписать в данную сферу.

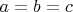
Приводим неравенство Коши и его следствие, из которого вытекает, что максимальный объём равен $8$ и достигается только в том случае, если $a=b=c$, то есть данный параллелепипед является кубом.

4)Итак, площадь полной поверхности $S = 2(ab+bc+ac) = 2(a^2 + b^2 + c^2) = 2 \cdot 12 = 24$.

Ответ: 24.

[Алексей К.]

Keter в сообщении #559793 писал(а):

Найдём параллелепипед максимально возможного объёма, который можно вписать в данную сферу.

В Вашем решении не хватает одной мелочи: надо было объяснить, почему это Вы вдруг решили искать ПП максимального объёма? А, видимо, потому, что Вы получили систему из двух уравнений с тремя неизвестными:

$$\begin{cases}a^2+b^2+c^2=12,\\ abc=8.\end{cases}$$

Больше зацепок нет. Задача похожа на имееющую бесконечно много решений. А всё же, от меня требуют её решить. Может, число 8 какое-то особенное?
Ведь ПП с $V=0$ ужас как много: $a=0, \; b=0,\; c=\sqrt{12}$; $a=0,\;b=c=\sqrt6$, и проч. А при $V=100$ решений, похоже, нет.
Дальше наклёвывается два пути:
1. Тот, по которому мы прошли: поискать уникальный ПП максимального объёма (убедиться в его уникальности!) и проверить: не его ли нам подсунули? Для этой догадки, видимо, требуется некий опыт решения задачек на максимум-минимум.
2. Тот, который мы не пробовали: поковырять всё же эту систему. А вдруг при таких правых частях окажется, что решение единственно? (Вариант: попытаться найти хотя бы два разных ПП, и доказать составителям, что они подсунули неправильную задачу. В процессе этого исследования, наверное, и обнаружилось бы, что...)

-- 14 апр 2012, 12:00:07 --

Ну и повторюсь: насколько я помню, параллелепипеды бывают не только прямоугольные. А от других мы как бы сразу молча отказались. Не знаю, требует ли формальное решение упоминания этого факта. Наверное, одно предложение на этот счёт не помешало бы.

-- 14 апр 2012, 12:12:30 --

Алексей К. в сообщении #559410 писал(а):

И только тогда мы имеем право сделать вывод, что, ежели нам задан прямоугольник такой именно площади, то он --- тот самый квадрат.

А здесь я малость лопухнулся: в двумерной задаче такой проблемы бы не было: там два уравнения с двумя неизвестными, и вписанный прямоугольник по заданному "объёму" (т.е. площади) определялся однозначно.

[Keter]

Наверное я бы объяснил поиск максимально возможного ПП тем, что мы должни проверить какой максимальный объём, вдруг он нам и дан, тогда задача упрощается и имеет единственное решение.

С системкой можно поиграть, может что и выйдет.

Ну а на счет того, что ПП не только прямоугольные бывают, то по моему есть правило, которое говорит, что сферу возможно описать только около прямоугольной призмы.

[ewert]

Keter в сообщении #559923 писал(а):

есть правило, которое говорит, что сферу возможно описать только около прямоугольной призмы.

Просто-напросто в сферу невозможно вписать параллелограмм, если он не прямоугольный (он ведь будет обязан вписаться в некоторую окружность).

[Keter]

ewert в сообщении #559928 писал(а):

Просто-напросто в сферу невозможно вписать параллелограмм, если он не прямоугольный (он ведь будет обязан вписаться в некоторую окружность).

Да, или так))

[AKM]

Keter в сообщении #559923 писал(а):

вдруг он нам и дан, тогда задача упрощается и имеет единственное решение.

Нет. Задача не "упрощается". Просто при $V=8$ тот текст действительно превращается в (интересную) задачу. Ведь при $V=6$ задачи просто нет. Ну, можно придумать слова, но...
Но никакого "упрощения" здесь нет. Только ратую за пущую строгость формулировок.