Да, только на будущее,
если имеется плотность распределения 
, то можно проще, без последующего использования функции распределения. Фактически, все сводится к тому, что вероятность любого события, связанного с попаданием значения с.в.
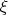
в произвольный интервал

в этом случае считается по формуле:

Вот ее стоит запомнить и применять в дальнейшем. Например, в вашем варианте
![$$\mathrm{P}(A_1) = \mathrm{P}(\xi \in [0,1]) = \int_{[0,1]}\frac{1}{4}\, dx = \frac{1}{4} (1 - 0) = \frac{1}{4}.$$ $$\mathrm{P}(A_1) = \mathrm{P}(\xi \in [0,1]) = \int_{[0,1]}\frac{1}{4}\, dx = \frac{1}{4} (1 - 0) = \frac{1}{4}.$$](https://dxdy-04.korotkov.co.uk/f/7/1/1/7117c52781cbf2cc46c2e57ccea9aaac82.png)
Обычный порядок таков - находят функцию распределения

через вероятность события
![$\xi \in (-\infty, x]$ $\xi \in (-\infty, x]$](https://dxdy-04.korotkov.co.uk/f/3/3/b/33b75757a02f5dde368f90b9cff87d9482.png)
, пользуясь соотношением
![$F_\xi(x) = \mathrm{P}(\xi \in (-\infty, x])$ $F_\xi(x) = \mathrm{P}(\xi \in (-\infty, x])$](https://dxdy-01.korotkov.co.uk/f/8/6/a/86a6f5f20acd50b7849d1d06a9ab591382.png)
. Далее, находят плотность

(если она существует!), пользуясь соотношением

. И дальше для вычисления интересующих вероятностей событий работают уже только с плотностью.
Ладно, идем дальше. Теперь нужно определиться с тем, что означает фраза "положение точки на окружности распределено равномерно". А означает она, что вероятность попадания точки в любую дугу на а этой окружности равна отношению длины дуги ко всей длине окружности.
В качестве закрепляющего дополнительного задания:
как вы знаете, положение точки на окружности фиксированного радиуса

можно однозначно задать углом

. Значит, если положение точки является равномерно распределенной по окружности случайной величиной, то и угол

будет тоже случайной величиной. С учетом сказанного, попытайтесь найти плотность распределения этой случайной величины

по указанной ранее схеме: найти функцию распределения

, а затем, продифференцировав ее, найти плотность

.
Справитесь, можете воспользоваться результатом, чтобы найти искомые вероятности попадания точки в заданные углы. Не справитесь - тоже ничего страшного (сделаете тогда как-нибудь позднее), можете, напрямую попытаться вычислить вероятности нужных событий.
В любойм случае, возвращаемся к вычислению вероятности события
Тогда вот так:
![$\varphi_C\in(-\frac{\pi}{2}, \arctg\frac{x}{a}]\cup(-\pi, -\frac{3\pi}{2}+\arctg\frac{x}{a}]$ $\varphi_C\in(-\frac{\pi}{2}, \arctg\frac{x}{a}]\cup(-\pi, -\frac{3\pi}{2}+\arctg\frac{x}{a}]$](https://dxdy-04.korotkov.co.uk/f/3/a/b/3ab167a296ce07633b8b7a9afe3922c982.png)