задача условной оптимизации графическим методом

[Praded]

Sverest в сообщении #554808 писал(а):

а как определили, что:

При этих значениях квадраты равны 0.

Sverest в сообщении #554808 писал(а):

так надо же не просто абсолютный минимум, а минимум при вышеперечисленных условиях

Вот в этом и проблема.

[Sverest]

а как уравнение эллипса привести к виду: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

[Sverest]

Praded в сообщении #554819 писал(а):

а как определили, что:
При этих значениях квадраты равны 0.

так это разве значит, что это минимум, это же просто координаты эллипса, а минимум будет в точке соприкосновения эллипса с заштрихованной площадью

то есть надо решить систему из уравнения эллипса и уравнения прямой, до которой касается эллипс?

[Praded]

Sverest в сообщении #554908 писал(а):

так это разве значит, что это минимум,

Минимум от глобального минимума отличаете?
Про точку соприкосновения изображения целевой функции и ограничивающей области понимаете верно.

[Sverest]

Praded в сообщении #554914 писал(а):

Минимум от глобального минимума отличаете?

Глобальный минимум - у всей функции
просто минимум - на каком то промежутке

[Sverest]

Вот так пример с окружностью разобран в методичке:

Цитата:

$f(x) = (x_1 - 3)^2 + (x_2 - 4)^2$

при условии
$3x_1 + 2x_2 \ge 7,\\ 10x_1 - x_2 \le 8,\\ -18x_1 + 4x_2 \le 12,\\ x_1,x_2 \ge 0.\\ $



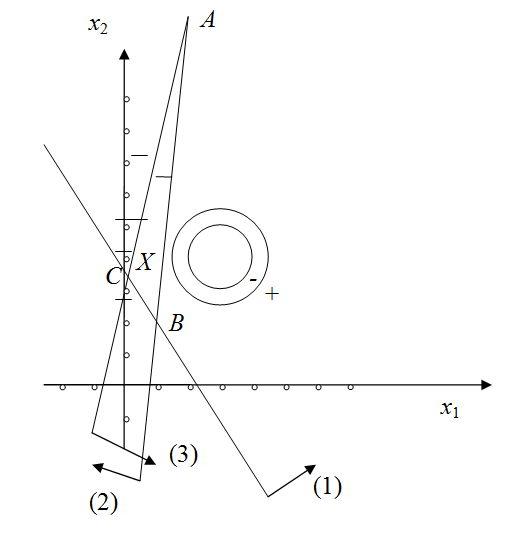
Для нахождения координат точки минимума воспользуемся равенством угловых коэффициентов прямой $10 x_1 - x_2 = 8$ и касательной к окружности в точке касания. Из уравнения прямой $10x_1 - 8 = x_2$ находим, что ее угловой коэффициент равен $10$. Угловой коэффициент касательной к окружности определим как значение производной функции $x_2$ от переменной $x_1$ в точке касания. Функция $x_2$ задана неявно, поэтому, дифференцируя уравнение окружности по переменной $x_1$, получим

$2(x_1 - 3) +2 (x_2 - 4)x_2 ' = 0,$
откуда
$x_2 ' = - \frac{(x_1 - 3)}{(x_2 - 4)}$

Приравнивая найденное выражение числу $10$, получим одно из уравнений для нахождения координат точки минимума целевой функции. Присоединяя к нему уравнение прямой, на которой лежит точка касания, получим систему уравнений для нахождения точки минимума
$-\frac{(x_1 - 3)}{(x_2 - 4)}=10$
$10 x_1-x_2=8$

С эллипсом такое наверно нельзя сделать, у него же касательные не перпендикулярны радиусу?

[Praded]

А там точно $2x_{2}^2$ ? Нет опечатки в виде лишней 2 ?

[Sverest]

Praded в сообщении #554947 писал(а):

А там точно $2x_{2}^2$ ? Нет опечатки в виде лишней 2 ?

опечатки нет

[ИСН]

значит, ищите касательную. в конце концов, там не может быть ничего сложнее квадратного уравнения.

-- Пн, 2012-04-02, 21:14 --

Тьфу, чёрт, что я несу. Не надо никаких касательных. Тупо найдите минимумы на всех границах и сравните их друг с другом.

[Sverest]

$\begin{cases} (x_1 -8)^2 +2 (x_2-5)^2-114= \\ 2x_2+x_2=16 \end{cases}$

а в верхнем уравнении после равно $0 $ ставить?

[ИСН]

А оно равно? А продукты с полки в корзинку класть? А деньги тётеньке отдавать?

[Sverest]

В примере в методичке $10$ ставили, но там была окружность же

Как определять что ставить?

[ИСН]

Смотря что мы хотим. А что мы хотим?

[Sverest]

координаты точки в которой эллипс соприкасается с прямой

[ИСН]

Какой эллипс?