Читаю учебник и запутался напрочь

Пусть

-- гладкое отображение многообразий,

,

. Я знаю, что такое дифференциал

. А что такое градиент

? Везде пишут по-разному. Моя попытка найти компромисс следующая (прошу исправить, если бред):
Так как

, то градиент -- это тот же дифференциал, только с изменённой областью прибытия. То есть градиент -- это функционал (= ковектор) из

. Если у нас есть скалярное произведение, то мы можем найти ему соответствующий вектор

из
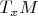
такой, что

. В декартовых координатах он будет иметь такие же координаты, как у градиента. Вот этот

подразумевают в классических учебниках под градиентом, его поле рисуют на всяких картах и т.п.

