А это точно не частный случай неравенства Караматы? (Тут объяснение приводится -
http://kvant.mccme.ru/pdf/2000/04/kv0400nomir.pdf)
2) Равенство

также не предполагается.
Достаточно рассмотреть случай

(Если несколько последних иксов равны 0, то отбросив их и столько же последних игреков уменьшим сумму

и не изменим сумму

И, т.к. для "урезанных" сумм неравенство выполнено, то оно выполнено и для исходных сумм.)
Пусть

Возьмём такое

что

и дополним наборы числами

и

Заметим, что условия

; и

выполнены и для нового неравенства, и кроме того

И, поскольку

то если неравенство выполнено для нового набора, то оно выполнено и для исходного.
1) Здесь ничего не говорится об упорядоченности набора

.
Если набор

упорядочить по убыванию, то условия

снова будут выполняться. Поэтому достаточно доказать утверждение для упорядоченных наборов.
3) Самый интересный момент - доказательство равенства наборов в случае
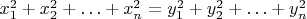
.
Заметим, что если наборы

и

не совпадают, то набор

строго мажорирует (т.е. мажорирует и не совпадает с ним) набор

И, поскольку функция

строго выпуклая, то выполнено строгое неравенство

А значит и строгое неравенство




