Треугольные неравенства

[Dave]

Функции $f(x)$ и $g(x)$ определены и непрерывны на отрезке $[a,b]$. Кроме этого, известно, что функция $f(x)$ - невозрастающая на этом отрезке, $f(b) \geqslant 0$, и для любого $c \in [a,b]$:

$$\int\limits_a^c f(x) dx \leqslant \int\limits_a^c g(x) dx.$$

Докажите, что для любого $c \in [a,b]$:

$$\int\limits_a^c f^2(x) dx \leqslant \int\limits_a^c g^2(x) dx.$$

[Dave]

Также докажите, что если, помимо этого, второе неравенство обращается в равенство при $c=b$, то $f(x) \equiv g(x)$ на всём отрезке $[a,b]$.

[Dave]

Тем, кто боится (или не знает) такого понятия, как интеграл, а также всем остальным, предлагаю взамен доказать следующий, не менее интересный, дискретный аналог вышеуказанных утверждений.

Числа $x_1 \geqslant x_2 \geqslant \dots \geqslant x_n \geqslant 0$, а также $y_1, y_2, \dots, y_n$ удовлетворяют неравенствам:

$\begin{array}{ll} x_1 & \leqslant y_1 \\ x_1+x_2 & \leqslant y_1+y_2 \\ x_1+x_2+x_3 & \leqslant y_1+y_2+y_3 \\ & \cdots \\ x_1+x_2+\ldots+x_n & \leqslant y_1+y_2+\ldots+y_n \end{array}$

Докажите, что справедливо также неравенство:

$x_1^2+x_2^2+\ldots+x_n^2 \leqslant y_1^2+y_2^2+\ldots+y_n^2$

и если оно обращается в равенство, то $x_i=y_i$ для любого $i=\overline {1,n}$.

[Nilenbert]

А это точно не частный случай неравенства Караматы? (Тут объяснение приводится - http://kvant.mccme.ru/pdf/2000/04/kv0400nomir.pdf)

[Dave]

Nilenbert в сообщении #545933 писал(а):

А это точно не частный случай неравенства Караматы? (Тут объяснение приводится - http://kvant.mccme.ru/pdf/2000/04/kv0400nomir.pdf)

Очень похоже, но разница есть:
1) Здесь ничего не говорится об упорядоченности набора $y=\{y_1,y_2,\dots,y_n\}$.
2) Равенство $x_1+x_2+\dots+x_n=y_1+y_2+\dots+y_n$ также не предполагается.
3) Самый интересный момент - доказательство равенства наборов в случае $x_1^2+x_2^2+\ldots+x_n^2=y_1^2+y_2^2+\ldots+y_n^2$.

[mihiv]

Предcтавим $g(x)=f(x)+\xi (x)$,тогда из условия следует,что $\int \limits _a^c\xi(x)dx\geqslant 0\qquad (1)$.Очевидно,что если $\xi (x)\geqslant 0$ для всех $x$,то нужное неравенство,выполняется.Рассмотрим поэтому случай,когда $\xi (x)$ меняет знак в некоторых точках отрезка [a,b].$i-$ю точку,в которой $\xi $ меняет знак с - на +,обозначим $c_i^+,i-$ю точку,в которой знак $\xi $,меняется с + на -,обозначим $c_i^-$.Точка $a=c_1^+$.
Покажем,что $I_i=\int \limits ^{c_i^+}_{c_1^+}f(x)\xi (x)dx\geqslant 0\qquad (2)$.

Т.к. функция $f$ не возрастает,то $I_1=\int \limits _{c_1^+}^{c_1^-}f(x)\xi (x)dx + \int \limits _{c_1^-}^{c_2^+}f(x)\xi (x)dx\geqslant f(c_1^-)\int \limits _{c_1^+}^{c_2^+}\xi (x)dx\geqslant 0,$(согласно (1)).Пусть уже доказано,что $I_k\geqslant f(c_k^-)\int \limits _{c_1^+}^{c_{k+1}^+}\xi (x)dx\geqslant 0$,тогда и

$$I_{k+1}\geqslant I_k+f(c_{k+1}^-)\int \limits _{c_{k+1}^+}^{c_{k+2}^+}\xi (x)dx\geqslant f(c_{k+1}^-)\int \limits _{c_1^+}^{c_{k+2}}\xi (x)dx\geqslant 0$$

Таким образом $\int \limits _{c_1^+}^{c_i^+}g^2(x)dx=\int \limits _{c_1^+}^{c_i^+}[f^2(x)+2f(x)\xi (x)+\xi ^2(x)]dx\geqslant \int \limits _{c_1^+}^{c_i^+}f^2(x)dx$,т.к. по доказанному интеграл от $f\xi $ неотрицателен.Равенство интегралов возможно только если $\xi (x)\equiv 0$.

[Dave]

mihiv в сообщении #546262 писал(а):

$i-$ю точку,в которой $\xi $ меняет знак с - на +,обозначим $c_i^+,i-$ю точку,в которой знак $\xi $,меняется с + на -,обозначим $c_i^-$.Точка $a=c_1^+$.

Но ведь возможен случай, когда $\xi$ меняет знак в бесконечном числе точек. Что-то типа $\xi(x)=x \sin\left(\frac 1 x \right)$ в окрестности нуля. Как тогда нумеровать?

[mihiv]

Dave в сообщении #546289 писал(а):

Но ведь возможен случай, когда $\xi$ меняет знак в бесконечном числе точек. Что-то типа $\xi(x)=x \sin\left(\frac 1 x \right)$ в окрестности нуля. Как тогда нумеровать?

Да,получается,что доказано только для функций $g,f$ таких,что функция $R(x)=g(x)-f(x)$ имеет лишь конечное число нулей на отрезке $[a,b]$.
Но зато для конечных сумм доказательство полностью годится.Так же представляем $y_i=x_i+\xi _i$,из условия следует,что $\sum \limits _{i=1}^l\xi _i\geqslant 0,l=1,\dots ,n;\sum y_i^2=\sum x_i^2+2x_i\xi _i+\xi _i^2$.Доказываем,что $\sum \limits _{i=1}^lx_i\xi _i\geqslant 0$ для всех $l$ и т.д.
Мне кажется,можно это обобщить и на ряды.

[hippie]

Dave в сообщении #545942 писал(а):

Nilenbert в сообщении #545933 писал(а):

А это точно не частный случай неравенства Караматы? (Тут объяснение приводится - http://kvant.mccme.ru/pdf/2000/04/kv0400nomir.pdf)

2) Равенство $x_1+x_2+\dots+x_n=y_1+y_2+\dots+y_n$ также не предполагается.

Достаточно рассмотреть случай $x_n>0.$
(Если несколько последних иксов равны 0, то отбросив их и столько же последних игреков уменьшим сумму $y_1^2+y_2^2+\ldots+y_n^2$ и не изменим сумму $x_1^2+x_2^2+\ldots+x_n^2.$ И, т.к. для "урезанных" сумм неравенство выполнено, то оно выполнено и для исходных сумм.)
Пусть $d=y_1+y_2+\dots+y_n-(x_1+x_2+\dots+x_n).$ Возьмём такое $k,$ что $x_n>\frac dk,$ и дополним наборы числами $x_{n+1}=x_{n+2}=\dots=x_{n+k}=x_n$ и $y_{n+1}=y_{n+2}=\dots=y_{n+k}=x_n-\frac dk.$
Заметим, что условия $x_1 \ge x_2 \ge \dots \ge x_{n+k} \ge 0$; и
$\begin{array}{ll} x_1 & \leqslant y_1 \\ x_1+x_2 & \leqslant y_1+y_2 \\ x_1+x_2+x_3 & \leqslant y_1+y_2+y_3 \\ & \cdots \\ x_1+x_2+\ldots+x_{n+k-1} & \leqslant y_1+y_2+\ldots+y_{n+k-1} \end{array}$
выполнены и для нового неравенства, и кроме того
$x_1+x_2+\dots+x_{n+k}=y_1+y_2+\dots+y_{n+k}.$
И, поскольку $x_{n+1}^2+x_{n+2}^2+\dots+x_{n+k}^2>y_{n+1}^2+y_{n+2}^2+\dots+y_{n+k}^2,$ то если неравенство выполнено для нового набора, то оно выполнено и для исходного.

Dave в сообщении #545942 писал(а):

1) Здесь ничего не говорится об упорядоченности набора $y=\{y_1,y_2,\dots,y_n\}$.

Если набор $\{y_1,y_2,\dots,y_{n+k}\}$ упорядочить по убыванию, то условия
$\begin{array}{ll} x_1 & \leqslant y_1 \\ x_1+x_2 & \leqslant y_1+y_2 \\ x_1+x_2+x_3 & \leqslant y_1+y_2+y_3 \\ & \cdots \\ x_1+x_2+\ldots+x_{n+k} & \leqslant y_1+y_2+\ldots+y_{n+k} \end{array}$
снова будут выполняться. Поэтому достаточно доказать утверждение для упорядоченных наборов.

Dave в сообщении #545942 писал(а):

3) Самый интересный момент - доказательство равенства наборов в случае $x_1^2+x_2^2+\ldots+x_n^2=y_1^2+y_2^2+\ldots+y_n^2$.

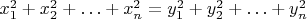
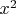
Заметим, что если наборы $\{x_1,x_2,\dots,x_n\}$ и $\{y_1, y_2,\dots,y_n\}$ не совпадают, то набор $\{y_1,y_2,\dots,y_{n+k}\}$ строго мажорирует (т.е. мажорирует и не совпадает с ним) набор $\{x_1,x_2,\dots,x_{n+k}\}.$ И, поскольку функция $x^2$ строго выпуклая, то выполнено строгое неравенство $y_1^2+y_2^2+\dots+y_{n+k}^2>x_1^2+x_2^2+\dots+x_{n+k}^2.$ А значит и строгое неравенство $y_1^2+y_2^2+\dots+y_n^2>x_1^2+x_2^2+\dots+x_n^2.$