|
alves |
Произведение роторов.  10.03.2012, 15:02 |
|
08/04/10
53
|
|
rot A * rot B
подскажите, чему это равно ?
|
|
|
|
 |
|
wallflower |
Re: Произведение роторов.  10.03.2012, 15:19 |
|
24/12/11
186
|
|
Зависит от того, что такое *
|
|
|
|
 |
|
alves |
Re: Произведение роторов.  10.03.2012, 15:20 |
|
08/04/10
53
|
|
|
|
 |
|
wallflower |
Re: Произведение роторов.  10.03.2012, 15:24 |
|
24/12/11
186
|
|
Ну так распишите по координатам роторы и скалярно умножьте.
|
|
|
|
 |
|
alves |
Re: Произведение роторов.  10.03.2012, 15:34 |
|
08/04/10
53
|
так никто не делает. надо например написать через символы Леви-Чивиты, но там у меня что-то странное поучается типа 
|
|
|
|
 |
|
dasalam |
Re: Произведение роторов.  10.03.2012, 16:01 |
|
02/05/09
49
|
так никто не делает. надо например написать через символы Леви-Чивиты, но там у меня что-то странное поучается типа  Делают и так. Как кому удобно. Откуда у вас взялись вторые производные?
|
|
|
|
 |
|
alves |
Re: Произведение роторов.  10.03.2012, 16:22 |
|
08/04/10
53
|
Последний раз редактировалось alves 10.03.2012, 16:28, всего редактировалось 1 раз.
из слагаемого 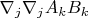 -- Сб мар 10, 2012 17:28:28 -- -- Сб мар 10, 2012 17:28:28 -- потом заменил  на  и получил что получил
|
|
|
|
 |
|
Himfizik |
Re: Произведение роторов.  10.03.2012, 17:15 |
|
31/10/10
404
|
и получил что получил Лапласиан произведения минус произведение дивергенций. Да, вроде правильно все у Вас. Даже простая проверка на случай  проходит успешно.
|
|
|
|
 |
|
мат-ламер |
Re: Произведение роторов.  10.03.2012, 20:25 |
|
| Заслуженный участник |
 |
30/01/09
7437
|
Последний раз редактировалось мат-ламер 10.03.2012, 20:28, всего редактировалось 1 раз.
В аналитической геометрии есть формула по преобразованию векторного произведения четырёх векторов (два векторных произведения и одно скалярное) через скалярные произведения (см. Берклеевский курс физики, механика, стр.69, формула 78).
|
|
|
|
 |
  |
Страница 1 из 1
|
[ Сообщений: 9 ] |
|
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы



