Может ли C(K) быть сопряжённым пространством?

[Oleg Zubelevich]

hippie
вот еще посмотрите, симпатичая статья: http://www.mscand.dk/article.php?id=2394

[g______d]

hippie в сообщении #545941 писал(а):

Позже я встречал значительно более общее утверждение:
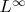
Каждое пространство $L^{\infty}$ изометрически изоморфно пространству $C(K),$ где $K$ — некоторый компакт.
(Доказательство воспроизвожу по памяти, и могу что-то упустить, поскольку материалом владею недостаточно.)
$L^{\infty} — полупростая коммутативная банахова алгебра. А каждая такая алгебра изоморфна некоторой алгебре $C(K),$ где $K$ — некоторый компакт.

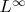
$L^{\infty}$ --- это не просто коммутативная банахова алгебра, это коммутативная $C^*$-алгебра с единицей. Категория таких алгебр эквивалентна категории компактных хаусдорфовых пространств.