Может ли C(K) быть сопряжённым пространством?

[hippie]

Существует ли такое бесконечное хаусдорфово компактное пространство $K,$ что $C(K)$ является сопряжённым к некоторому банахову пространству?

[Oleg Zubelevich]

Выкладывайте уже решение

[hippie]

Пока что ограничусь подсказкой.

Каждая непрерывная ограниченная (числовая) функция, заданная на тихоновском пространстве, единственным образом продолжается до функции непрерывной на стоун-чеховской компактификации этого пространства.

[Ktina]

hippie в сообщении #545319 писал(а):

Пока что ограничусь подсказкой.

Каждая непрерывная ограниченная (числовая) функция, заданная на тихоновском пространстве, единственным образом продолжается до функции непрерывной на стоун-чеховской компактификации этого пространства.

(Оффтоп)

Прошу прощения за оффтоп.
А на каком курсе это проходят? Я так понимаю, речь идёт либо о функане, либо об общей топологии.
У меня покамест возникли только три ассоциации с Вашей подсказкой - Штирлиц, "Основной инстинкт" и Каштанка

[Oleg Zubelevich]

hippie в сообщении #544895 писал(а):

Существует ли такое бесконечное хаусдорфово компактное пространство $K,$ что $C(K)$ является сопряжённым к некоторому банахову пространству?

Будем доказывать, что не существует.

Идея следующая. От противного, пусть $X$ -- банахово пространство и $X'=C(K)$, тогда $X''=(C(K))'$ -- пространство мер Радона на $K$. Имеется каноническое вложение $J:X\to X''$.
ПУсть $\{f_n\}\subset C(K)$ -- ограниченная последовательность функций поточечно сходящаяся к функции $f$ -- разрывной на $K$. Из общих теорем следует, что

$$(f_j-f_i,\mu)\to 0,\quad \mu\in X'',\quad i,j\to\infty\qquad (1).$$

При этом мы знаем, что $C(K)$ $*$-слабо полно (потому, что $X$ -- банахово). Поэтому беря в формуле (1)
$\mu\in J(X)$ мы должны получить $f\in C(K)$. Противоречие.

Я тут не доконца все продумал, но думаю, что если и есть пробелы, все можно довести до формального доказательства.

-- Пн мар 05, 2012 09:12:18 --

Подозреваю, что вместо $K$ можно брать любое отделимое локально компактное пространство на котором сущестуют разрывные функции

[Oleg Zubelevich]

Oleg Zubelevich в сообщении #545438 писал(а):

, что $C(K)$ $*$-слабо полно

слабо секвенциально полно

[Oleg Zubelevich]

Я свои рассуждения проверил, ошибок в доказательстве не нашел, считаю задачу решенной.
(Единственное, я не проверял, что на всяком бесконечном компакте найдется разрывная функция и последовательность непрерывных функций, которая к этой разрывной функции сходится поточено. Наверное, это из какой-нибудь вполне регулярности вытекает. Для метризуемых компактов это верно заведомо.)
Хотелось бы увидеть решение ТС, основанное на

hippie в сообщении #545319 писал(а):

Пока что ограничусь подсказкой.

Каждая непрерывная ограниченная (числовая) функция, заданная на тихоновском пространстве, единственным образом продолжается до функции непрерывной на стоун-чеховской компактификации этого пространства.

[Padawan]

Oleg Zubelevich в сообщении #545438 писал(а):

При этом мы знаем, что $C(K)$ $*$-слабо полно (потому, что $X$ -- банахово). Поэтому беря в формуле (1)
$\mu\in J(X)$ мы должны получить $f\in C(K)$. Противоречие.

Почему? Мы должны получить, что существует некоторая функция $g\in C(K)$ такая, что $\lim\limits_{j\to\infty}(f_j,\mu)=(g,\mu)$ для любой меры $\mu\in J(X)$. Откуда следует, что $g=f$ ?

[Oleg Zubelevich]

Да, действительно.

[hippie]

Oleg Zubelevich в сообщении #545438 писал(а):

Будем доказывать, что не существует.

Лучше будем доказывать, что существует .

Поскольку каждая непрерывная ограниченная функция, заданная на тихоновском пространстве $X,$ единственным образом продолжается до непрерывной функции на $\beta X$ (стоун-чеховской компактификации $X$), то между пространствами $BC(X)$ (ограниченных непрерывных функций на $X$ с sup-нормой) и $C(\beta X)$ существует естественная биекция. А именно — продолжение ограниченной непрерывной функции заданной на $X$ до непрерывной функции на $\beta X$ (или наоборот — ограничение на $X$ функции непрерывной на $\beta X$). Поскольку при этой биекции сохраняются линейные операции и норма, то пространства $BC(X)$ и $C(\beta X)$ изометрически изоморфны.
Таким образом:

$$C(\beta\mathbb{N})=BC(\mathbb{N})=l^{\infty}=\left(l^1\right)^*.$$

(Оффтоп)

Ktina в сообщении #545362 писал(а):

Я так понимаю, речь идёт либо о функане, либо об общей топологии.

Точнее речь идёт И о функане И о топологии. Стоун-чеховская компактификация относится к топологии, всё остальное — это функан.

Ktina в сообщении #545362 писал(а):

У меня покамест возникли только три ассоциации с Вашей подсказкой - Штирлиц, "Основной инстинкт" и Каштанка.

Насчёт "Основного инстинкта" не знаю — никогда не смотрел и не знаю о чём это. А с "Каштанкой" ассоциация неправильная. "Чеховская" это от фамилии "Чех", а не "Чехов".

[Oleg Zubelevich]

hippie в сообщении #545772 писал(а):

Поскольку каждая непрерывная ограниченная функция, заданная на тихоновском пространстве $X,$ единственным образом продолжается до непрерывной функции на $\beta X$ (стоун-чеховской компактификации $X$), то между пространствами $BC(X)$ (ограниченных непрерывных функций на $X$ с sup-нормой) и $C(\beta X)$ существует естественная биекция. А именно — продолжение ограниченной непрерывной функции заданной на $X$ до непрерывной функции на $\beta X$ (или наоборот — ограничение на $X$ функции непрерывной на $\beta X$). Поскольку при этой биекции сохраняются линейные операции и норма, то пространства $BC(X)$ и $C(\beta X)$ изометрически изоморфны.
Таким образом:

$$C(\beta\mathbb{N})=BC(\mathbb{N})=l^{\infty}=\left(l^1\right)^*.$$

Здорово!. Ответ задачи совершенно противоречил моей интуиции

[Padawan]

hippie в сообщении #545772 писал(а):

Oleg Zubelevich в сообщении #545438 писал(а):

Будем доказывать, что не существует.

Лучше будем доказывать, что существует .

Поскольку каждая непрерывная ограниченная функция, заданная на тихоновском пространстве $X,$ единственным образом продолжается до непрерывной функции на $\beta X$ (стоун-чеховской компактификации $X$), то между пространствами $BC(X)$ (ограниченных непрерывных функций на $X$ с sup-нормой) и $C(\beta X)$ существует естественная биекция. А именно — продолжение ограниченной непрерывной функции заданной на $X$ до непрерывной функции на $\beta X$ (или наоборот — ограничение на $X$ функции непрерывной на $\beta X$). Поскольку при этой биекции сохраняются линейные операции и норма, то пространства $BC(X)$ и $C(\beta X)$ изометрически изоморфны.
Таким образом:

$$C(\beta\mathbb{N})=BC(\mathbb{N})=l^{\infty}=\left(l^1\right)^*.$$

Ого... Прикольно. А я то все думаю, почему не получается доказать, что не существует . Все-таки стоун-чеховская компактификация, даже просто $\beta \mathbb N$ -- хорошая штука.

-- Вт мар 06, 2012 16:07:30 --

Встает вопрос, а если $K$ -- метрический компакт?

[Oleg Zubelevich]

Padawan в сообщении #545806 писал(а):

Встает вопрос, а если $K$ -- метрический компакт?

мне почему-то кажется, что мы надорвемся уже на пространстве $C[0,1]$

[sup]

кажется, насчет $C[0,1]$ уже было http://dxdy.ru/topic37333.html

[hippie]

Oleg Zubelevich в сообщении #545777 писал(а):

Ответ задачи совершенно противоречил моей интуиции

Мне в этом повезло больше. Мысль рассматривать $l^{\infty}$ как $C(\beta \mathbb{N})$ у меня возникла в связи с задачей как описать пространство $\left(l^{\infty}\right)^*.$ Поэтому, когда я впервые столкнулся с вопросом "может ли пространство $C(K)$ быть сопряжённым к чему-нибудь", у меня уже был готовый ответ.

Позже я встречал значительно более общее утверждение:
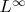
Каждое пространство $L^{\infty}$ изометрически изоморфно пространству $C(K),$ где $K$ — некоторый компакт.
(Доказательство воспроизвожу по памяти, и могу что-то упустить, поскольку материалом владею недостаточно.)
$L^{\infty} — полупростая коммутативная банахова алгебра. А каждая такая алгебра изоморфна некоторой алгебре $C(K),$ где $K$ — некоторый компакт.

Oleg Zubelevich в сообщении #545851 писал(а):

Padawan в сообщении #545806 писал(а):

Встает вопрос, а если $K$ — метрический компакт?

мне почему-то кажется, что мы надорвемся уже на пространстве $C[0,1]$

Если рассматривать пространства над $\mathbb{R}$, то не надорвёмся.
Если пространство является сопряжённым, то единичный замкнутый шар *-слабо компактен, и, следовательно (по теореме Крейна–Мильмана), является замыканием выпуклой оболочки своих крайних точек. Но в $C[a;\ b]$ есть только 2 крайние точки, и их выпуклая оболочка это константы.
Такое же доказательство проходит для всех компактов, имеющих компоненты связности, состоящие более чем из одной точки.
По-моему, намного интереснее разобраться с канторовым множеством.