Гамильтонова редукция
Пусть на

-мерном(симплектическом) многообразии

задан Гамильтониан

и какой-нибудь интеграл движения

:

. Существует такое каноническое преобразование координат

что

где

- новая переменная сопряженная новому импульсу

(который совпадает с интегралом движения).
Скобка Пуассона любых двух величин

и

(

) зависит от новых координат

и импульса

. Т.к. последний сохраняется, мы можем зафиксировать его значение равным константе

. Новый траектории нового Гамильтониана будут проекциями тректории старого при заданном граничном условии

. Процедура описанная выше называется Гамильтоновой редукцией а новый
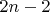
-мерный Гамильтониан

-редуцированным Гамильтонианом.
Вопрос
Пусть поверхность уровня

задается уравнением

.
Что умного можно сказать про поверхность уровня

?
Например, что существует расслоение

.
-- Чт фев 02, 2012 14:51:53 --Вопрос 2
Пусть кроме

существуют

(

) интегралов движения

, которые, однако, не коммутируют с

. Как определить, существует ли функция

коммутирующая с

и сколько таких функционально независимых функций?
P.S.
Не знаю важно ли, но у меня интегралы движения

образуют алгебру Ли:

.



